Cho tam giác MNP có \(\widehat M = 63^\circ ,\widehat N = 48^\circ \). Vẽ trực tâm O của tam giác MNP. Số đo góc MON là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Gọi giao điểm của NO và PM là A, giao điểm của MO và PN là B
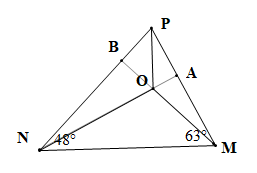
Vì O là trực tâm tam giác MNP nên NA ⊥ PM, MB ⊥ PN.
Vì DMNA vuông tại A nên \(\widehat {ANM} + \widehat {AMN} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {ANM} = 90^\circ - \widehat {AMN} = 90^\circ - 63^\circ = 27^\circ \).
Vì DMNB vuông tại B nên \(\widehat {BNM} + \widehat {BMN} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {BMN} = 90^\circ - \widehat {BNM} = 90^\circ - 48^\circ = 42^\circ \).
Xét DOMN có \(\widehat {ONM} + \widehat {OMN} + \widehat {MON} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {MON} = 180^\circ - \widehat {ONM} - \widehat {OMN} = 180^\circ - 27^\circ - 42^\circ = 111^\circ \).
Vậy ta chọn phương án A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
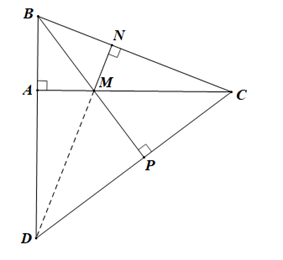
• Xét ∆DBC có CA, BP là hai đường cao cắt nhau tại M nên M là trực tâm của ∆DBC.
Do đó phương án A đúng.
• Vì M là trực tâm của ∆DBC nên DM ⊥ BC.
Do đó phương án B đúng.
• Ta có DM ⊥ BC (chứng minh trên).
Mà MN ⊥ BC (giả thiết).
Suy ra D, M, N thẳng hàng.
Do đó phương án C đúng.
• Ta có:
+) D ∈ MN (do D, M, N thẳng hàng);
+) D ∈ AB (giả thiết);
+) D ∈ CP (giả thiết).
Suy ra AB, MN, CP cùng đồng quy tại điểm D.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
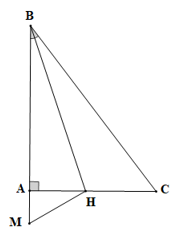
• Xét ΔBHM và ∆BHC có:
BH là cạnh chung,
\(\widehat {ABH} = \widehat {CBH}\) (do BH là tia phân giác của góc ABC),
BM = BC (giả thiết)
Do đó ΔBHM = ∆BHC (c.g.c)
Suy ra MH = HC (hai cạnh tương ứng), nên C là khẳng định đúng.
• Vì BM = BC và HM = HC nên BH là đường trung trực của MC.
Do đó BH ⊥ MC hay BH là đường cao của tam giác MBC.
Khi đó A là khẳng định đúng.
• Xét DBMC có hai đường cao BH và CA cắt nhau tại H nên H là trực tâm tam giác BMC.
Do đó MH ⊥ BC nên khẳng định B là đúng.
Vậy ta chọn phương án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập