Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G.
Cho các phát biểu sau:
(I) \[AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\];
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
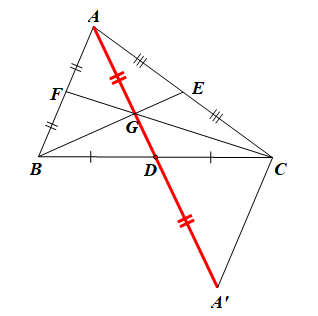
• Ta xét (I):
Vì G là trọng tâm của ∆ABC nên ta có \(GB = \frac{2}{3}BE\) và \(GC = \frac{2}{3}CF\).
∆GBC có GB + GC > BC (bất đẳng thức tam giác).
Suy ra \(\frac{2}{3}BE + \frac{2}{3}CF > BC\).
Hay \(\frac{2}{3}\left( {BE + CF} \right) > BC\).
Do đó \(BE + CF > \frac{3}{2}BC\) (1).
Chứng minh tương tự ta được:
+) \(AD + BE > \frac{3}{2}AB\) (2).
+) \(AD + CF > \frac{3}{2}AC\) (3).
Lấy (1) + (2) + (3) vế theo vế, ta được:
\(2AD + 2BE + 2CF > \frac{3}{2}AB + \frac{3}{2}BC + \frac{3}{2}AC\).
Suy ra \(2\left( {AD + BE + CF} \right) > \frac{3}{2}\left( {AB + BC + AC} \right)\).
Do đó \(AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\).
Vậy (I) đúng.
• Ta xét (II):
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.
Xét ∆ADB và ∆A’DC, có:
DA = DA’,
\(\widehat {ADB} = \widehat {A'DC}\) (hai góc đối đỉnh),
BD = CD (do AD là đường trung tuyến của ∆ABC),
Do đó ∆ADB = ∆A’DC (c.g.c).
Suy ra AB = A’C (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được:
AA’ < AC + A’C.
Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).
Chứng minh tương tự, ta được:
+) 2BE < AB + BC (5).
+) 2CF < AC + BC (6).
Lấy (4) + (5) + (6) vế theo vế, ta được:
2AD + 2BE + 2CF < 2AC + 2AB + 2BC.
Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).
Do đó AD + BE + CF < AB + AC + BC.
Vậy (II) đúng.
Kết luận: cả (I) và (II) đều đúng.
Ta chọn phương án C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
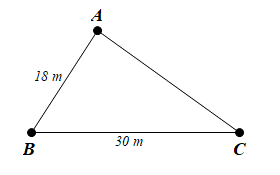
Theo bất đẳng thức ta có:
BC – AB < AC < BC + AC
Hay 30 – 18 < AC < 30 + 18
Suy ra 12 < AC < 48
Nếu đặt ở khu vực A một thiết bị phát wifi đảm bảo cả hai khu vực B và C đều nhận được tín hiệu thì bán kính hoạt động cần lớn hơn khoảng cách AB và AC.
Do đó trong các bán kính hoạt động của thiết bị phát wifi được nêu ở các phương án thì bán kính hợp lí là 48 m.
Ta chọn phương án D.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
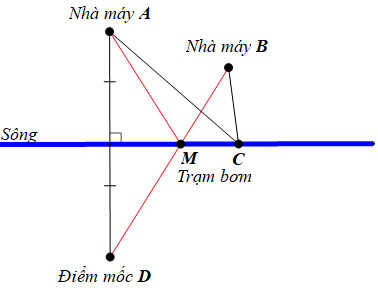
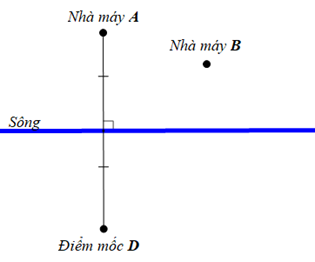
Vì D là điểm đối xứng của A qua bờ sông
Nên bờ sông chính là đường trung trực của AD.
Do đó CA = CD (tính chất đường trung trực)
Suy ra CA + CB = CD + CB.
Gọi M là giao điểm của BD và bờ sông.
+) Nếu C không trùng với M, ta xét ∆BCD, có:
CB + CD > BD hay CA + CB > BD (1).
+) Nếu C trùng với M thì:
CA + CB = CD + CB = MD + MB = BD (2).
Từ (1), (2), ta suy ra CA + CB ≥ BD.
Do đó khi C trùng với M hay C là giao điểm của BD với bờ sông thì giá trị của tổng CA + CB là nhỏ nhất.
Vậy ta chọn phương án A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập