Câu hỏi:

31/01/2023 1,236

Trong không gian Oxyz, cho đường thẳng $d : \frac{x + 2}{4} = \frac{y - 1}{- 4} = \frac{z + 2}{3}$ và mặt phẳng $(P) : 2 x - y + 2 z + 1 = 0$ . Đường thẳng $∆$ đi qua $E (- 2; 1; - 2)$ , song song với $(P)$ có một vectơ chỉ phương $\vec{u} = (m; n; 1)$ , đồng thời tạo với d góc bé nhất. Tính $T = m^{2} - n^{2}$ .

A. $T = - 5$ .

T = 4

T = 3

T = - 4

Xem lời giải

Câu hỏi trong đề: 87 câu Chuyên đề Toán 12 Bài 3: Phương trình đường thẳng có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Mặt phẳng $(P)$ có vectơ pháp tuyến là $\vec{n} = (2; - 1; 2)$ ; đường thẳng d có vectơ chỉ phương là $\vec{v} = (4; - 4; 3)$ .

$Δ // (P) \Rightarrow \vec{u} ⊥ \vec{n} \Leftrightarrow 2 m - n + 2 = 0 \Leftrightarrow n = 2 m + 2$

Mặt khác ta có: $\cos (\hat{Δ; d}) = \frac{|\vec{u} . \vec{v}|}{|\vec{u}| |\vec{v}|} = \frac{|4 m - 4 n + 3|}{\sqrt{m^{2} + n^{2} + 1} . \sqrt{4^{2} + {(- 4)}^{2} + 3^{2}}}$

$= \frac{|4 m + 5|}{\sqrt{41 (5 m^{2} + 8 m + 5)}} = \frac{1}{\sqrt{41}} . \sqrt{\frac{{(4 m + 5)}^{2}}{5 m^{2} + 8 m + 5}} = \frac{1}{\sqrt{41}} . \sqrt{\frac{16 m^{2} + 40 m + 25}{5 m^{2} + 8 m + 5}}$

Vì $0 ° \leq (\hat{Δ, d}) \leq 90 °$ nên $(\hat{Δ, d})$ bé nhất khi và chỉ khi $\cos (\hat{Δ, d})$ lớn nhất.

Xét hàm số $f (t) = \frac{16 t^{2} + 40 t + 25}{5 t^{2} + 8 t + 5} \Rightarrow f^{'} (t) = \frac{- 72 t^{2} - 90 t}{{(5 t^{2} + 8 t + 5)}^{2}}$ .

Bảng biến thiên:

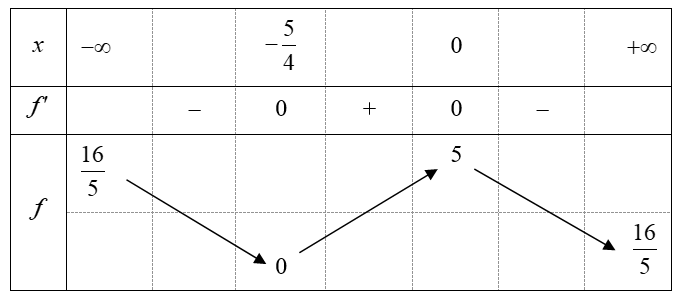
Dựa vào bảng biến thiên ta có: $\max f (t) = f (0) = 5$ .

Suy ra $(\hat{Δ, d})$ bé nhất khi $m = 0 \Rightarrow n = 2$ .

Do đó $T = m^{2} - n^{2} = - 4$ .

Chọn D.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, d là đường thẳng đi qua điểm A(1,-1,2), song song với mặt phẳng $(P) : 2 x - y - z + 3 = 0$ , đồng thời tạo với đường thẳng $Δ : \frac{x + 1}{1} = \frac{y - 1}{- 2} = \frac{z}{2}$ một góc lớn nhất. Phương trình đường thẳng d là

A. $\frac{x - 1}{- 4} = \frac{y + 1}{5} = \frac{z - 2}{3}$ .

\frac{x - 1}{4} = \frac{y + 1}{- 5} = \frac{z - 2}{3}

\frac{x + 1}{4} = \frac{y + 1}{5} = \frac{z - 2}{- 3}

\frac{x - 1}{4} = \frac{y + 1}{5} = \frac{z - 2}{3}

Lời giải

Mặt phẳng $(P) : 2 x - y - z + 3 = 0$ có một vectơ pháp tuyến là ${\vec{n}}_{_{(P)}} = (2; - 1; - 1)$ .

Đường thẳng $Δ : \frac{x + 1}{1} = \frac{y - 1}{- 2} = \frac{z}{2}$ có một vectơ chỉ phương là ${\vec{u}}_{_{Δ}} = (1; - 2; 2)$ .

Giả sử đường thẳng d có vectơ chỉ phương là ${\vec{u}}_{_{d}}$ .

Do $0 ° \leq (d, Δ) \leq 90 °$ mà theo giả thiết d tạo $∆$ góc lớn nhất nên $(d, Δ) = 90 ° \Rightarrow {\vec{u}}_{d} ⊥ {\vec{u}}_{Δ}$ .

Lại có $d // (P)$ nên ${\vec{u}}_{d} ⊥ {\vec{n}}_{(P)}$ . Do đó chọn ${\vec{u}}_{d} = [{\vec{u}}_{Δ}, {\vec{n}}_{(P)}] = (4; 5; 3)$ .

Vậy phương trình đường thẳng d là $\frac{x - 1}{4} = \frac{y + 1}{5} = \frac{z - 2}{3}$ .

Chọn D.

Câu 2

Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng $(P) : x - z . \sin α + \cos α = 0; (Q) : y - z . \cos α - \sin α = 0; α \in (0; \frac{π}{2})$ .

Góc giữa d và trục Oz là:

A. $30 °$ .

45 °

60 °

90 °

Lời giải

Mặt phẳng $(P)$ có vectơ pháp tuyến là $\vec{n_{(P)}} = (1; 0; - \sin α)$ .

Mặt phẳng $(Q)$ có vectơ pháp tuyến là $\vec{n_{(Q)}} = (0; 1; - \cos α)$ .

d là giao tuyến của (P) và (Q) nên vectơ chỉ phương của d là:

$\vec{u_{(d)}} = [\vec{n_{(P)}}, \vec{n_{(Q)}}] = (\sin α; \cos α; 1)$

Vectơ chỉ phương của (Oz) là $\vec{u_{(O z)}} = (0; 0; 1)$ .

Suy ra $\cos (d, O z) = \frac{|0. \sin α + 0. \cos α + 1.1|}{\sqrt{\sin^{2} α + \cos^{2} α + 1^{2}} . \sqrt{0 + 0 + 1^{2}}} = \frac{1}{\sqrt{2}} \Rightarrow (d, O z) = 45 °$ .

Vậy góc giữa d và trục $(O z)$ là $45 °$ .

Chọn B.

Câu 3

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x - 2}{1} = \frac{y - 1}{- 2} = \frac{z + 1}{3}$ và mặt phẳng $(α) : - x + 2 y - 3 z = 0$ . Gọi $φ$ là góc giữa đường thẳng d và mặt phẳng $(α)$ . Khi đó góc $φ$ bằng

A. $0 °$ .

45 °

90 °

60 °

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian Oxyz, cho hai đường thẳng $Δ_{1} : \frac{x - 1}{- 2} = \frac{y + 2}{1} = \frac{z - 3}{2}$ và $Δ_{2} : \frac{x + 3}{1} = \frac{y - 1}{1} = \frac{z + 2}{- 4}$ . Góc giữa hai đường thẳng $Δ_{1}, Δ_{2}$ bằng

A. $30 °$ .

45 °

60 °

135 °

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z + 2)}^{2} = 4$ và đường thẳng $d : \{\begin{cases} x = 2 - t \\ y = t \\ z = m - 1 + t \end{cases}$ .

Tổng tất cả các giá trị thực của tham số m để d cắt (S) tại hai điểm phân biệt A,B và các mặt phẳng tiếp diện của (S) tại A,B tạo với nhau một góc lớn nhất bằng

A. -1,5.

B. 3.

C. -3.

D. -2,25.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, hai đường thẳng $d_{1} : \frac{x - 2}{1} = \frac{y + 1}{\sqrt{2}} = \frac{z - 3}{1}$ và $d_{2} : \frac{x + 5}{1} = \frac{y + 3}{\sqrt{2}} = \frac{z - 5}{m}$ tạo với nhau góc $60 °$ , giá trị của tham số m bằng

A. $m = - 1$ .

m = \frac{\sqrt{3}}{2}

m = \frac{1}{2}

m = 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng $(P) : x - z . \sin α + \cos α = 0; (Q) : y - z . \cos α - \sin α = 0; α \in (0; \frac{π}{2})$ .

Góc giữa d và trục Oz là:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x - 2}{1} = \frac{y - 1}{- 2} = \frac{z + 1}{3}$ và mặt phẳng $(α) : - x + 2 y - 3 z = 0$ . Gọi $φ$ là góc giữa đường thẳng d và mặt phẳng $(α)$ . Khi đó góc $φ$ bằng

Trong không gian Oxyz, cho hai đường thẳng $Δ_{1} : \frac{x - 1}{- 2} = \frac{y + 2}{1} = \frac{z - 3}{2}$ và $Δ_{2} : \frac{x + 3}{1} = \frac{y - 1}{1} = \frac{z + 2}{- 4}$ . Góc giữa hai đường thẳng $Δ_{1}, Δ_{2}$ bằng

Trong không gian Oxyz, hai đường thẳng $d_{1} : \frac{x - 2}{1} = \frac{y + 1}{\sqrt{2}} = \frac{z - 3}{1}$ và $d_{2} : \frac{x + 5}{1} = \frac{y + 3}{\sqrt{2}} = \frac{z - 5}{m}$ tạo với nhau góc $60 °$ , giá trị của tham số m bằng