Giải phương trình lượng giác sau: \[{\sin ^2}\left( {\frac{x}{2}} \right) - 2{\cos ^2}\left( {\frac{x}{4}} \right) + \frac{3}{4} = 0\].

Phương pháp:

- Tính số phần tử không gian mẫu \[n\left( \Omega \right)\]

- Tính số khả năng có lợi cho biến cố \[A\] đã cho.

- Tính xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\].

Cách giải:

Chọn 4 trong 16 quả cầu, \[n\left( \Omega \right) = C_{16}^4 = 1820\].

Gọi \[A\] là biến cố: “Có đúng 1 quả cầu đỏ và không quá 2 quả cầu vàng”

TH1: Chọn được 1 quả cầu đỏ, 2 quả cầu vàng, 1 quả cầu xanh có \[C_4^1.C_7^2.C_5^1 = 420\] cách.

TH2: Chọn được 1 quả cầu đỏ, 1 quả cầu vàng, 2 quả cầu xanh có \[C_4^1.C_7^1.C_5^2 = 280\] cách.

TH3: Chọn được 1 quả cầu đỏ, 0 quả cầu vàng, 3 quả cầu xanh có \[C_4^1.C_7^0.C_5^3 = 40\] cách.

Do đó \[n\left( A \right) = 420 + 280 + 40 = 740\].

Xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{740}}{{1820}} = \frac{{37}}{{91}}\].

Phương pháp:

a) Sử dụng định lí ba giao tuyến song song: \[\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( \beta \right) = {d_1}\\\left( \beta \right) \cap \left( \gamma \right) = {d_2}\\\left( \alpha \right) \cap \left( \gamma \right) = {d_3}\\{d_1}//{d_2}\end{array} \right. \Rightarrow {d_3}//{d_1}//{d_2}\].

Cách giải:

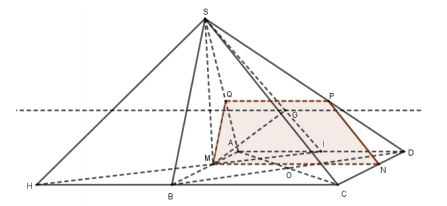
1) Tìm giao tuyến của mặt phẳng \[\left( {SAD} \right)\] và mặt phẳng \[\left( {GBC} \right)\]. Tìm giao điểm \[H\] của đường thẳng \[BC\] với mặt phẳng \[\left( {SGM} \right)\].

Dễ thấy \[G \in \left( {GBC} \right) \cap \left( {SAD} \right)\].

Xét các mặt phẳng: \[\left( {GBC} \right),{\rm{ }}\left( {SAD} \right),{\rm{ }}\left( {ABCD} \right)\] có:

\[\left\{ \begin{array}{l}\left( {GBC} \right) \cap \left( {SAD} \right) = Gx\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\\left( {ABCD} \right) \cap \left( {GBC} \right) = BC\\BC//AD\end{array} \right. \Rightarrow Gx//AB//CD\]

Vậy \[\left( {SAD} \right) \cap \left( {GBC} \right) = Gx\] là đường thẳng đi qua \[G\] và song song \[AD\].

Gọi \[I\] là trung điểm \[AD\], khi đó \[\left( {SGM} \right) \equiv \left( {SIM} \right)\].

Trong \[\left( {ABCD} \right)\], gọi \[H = IM \cap BC \Rightarrow \left\{ \begin{array}{l}H \in IM \subset \left( {SIM} \right)\\H \in BC\end{array} \right. \Rightarrow H = BC \cap \left( {SMG} \right)\].