Câu hỏi:

12/07/2024 3,224

Cho hàm số $y = f (x)$ có đạo hàm liên tục trên và bảng xét dấu đạo hàm như sau:

Hỏi hàm số $y = 3 f (- x^{4} + 4 x^{2} - 6) + 2 x^{6} - 3 x^{4} - 12 x^{2}$ có tất cả bao nhiêu điểm cực tiểu?

Xem lời giải

Câu hỏi trong đề: Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

$y^{'} = - (12 x^{3} - 24 x) . f^{'} (- x^{4} + 4 x^{2} - 6) + 12 x^{5} - 12 x^{3} - 24 x$

$= - 12 x (x^{2} - 2) . f^{'} (- x^{4} + 4 x^{2} - 6) + 12 x (x^{4} - x^{2} - 2)$

$= - 12 x (x^{2} - 2) . [f^{'} (- x^{4} + 4 x^{2} - 6) - (x^{2} + 1)]$

Ta có $- x^{4} + 4 x^{2} - 6 = - {(x^{2} - 2)}^{2} - 2 \leq - 2, \forall x \in ℝ$ .

Dựa vào bảng xét dấu .

Mà $x^{2} + 1 \geq 1, \forall x \in ℝ$ .

Do đó : $f' (- x^{4} + 4 x^{2} - 6) - (x^{2} + 1) < 0, \forall x \in ℝ$ .

+ Cho . $y' = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x_{2} - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm \sqrt{2} \end{array}$

Hàm số $y = 3 f (- x^{4} + 4 x^{2} - 6) + 2 x^{6} - 3 x^{4} - 12 x^{2}$ có bảng xét dấu đạo hàm như sau:

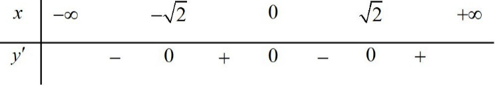
Cho hàm số y=f(x) có đạo hàm liên tục trên R và bảng xét dấu đạo hàm như sau: Hỏi hàm số y=3f( -x^4+4x^2-6)+2x^6-3x^4-12x^2 có tất cả bao nhiêu (ảnh 1)

Vậy hàm số $y = 3 f (- x^{4} + 4 x^{2} - 6) + 2 x^{6} - 3 x^{4} - 12 x^{2}$ có 2 điểm cực tiểu.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{5 x^{2} - 4 x - 1}{x^{2} - 1}$ là

A. 0

B. 1

C. 2

D. 3

Lời giải

Chọn C

· Vì $\lim_{x \to \pm \infty} \frac{5 x^{2} - 4 x - 1}{x^{2} - 1} = \lim_{x \to \pm \infty} \frac{x^{2} (5 - \frac{4}{x} - \frac{1}{x^{2}})}{x^{2} (1 - \frac{1}{x^{2}})} = \lim_{x \to \pm \infty} \frac{5 - \frac{4}{x} - \frac{1}{x^{2}}}{1 - \frac{1}{x^{2}}} = 5$ nên đồ thị hàm số có một tiệm cận ngang y=5 .

· Vì $\lim_{x \to 1} y = \lim_{x \to 1} \frac{5 x^{2} - 4 x - 1}{x^{2} - 1} = \lim_{x \to 1} \frac{(5 x + 1) (x - 1)}{(x + 1) (x - 1)} = \lim_{x \to 1} \frac{5 x + 1}{x + 1} = \frac{6}{2} = 3$ nên x=1 không là tiệm cận đứng của đồ thị hàm số.

· $\lim_{x \to {(- 1)}^{+}} y = \lim_{x \to {(- 1)}^{+}} \frac{5 x^{2} - 4 x - 1}{x^{2} - 1} = \lim_{x \to {(- 1)}^{+}} \frac{5 x^{2} - 4 x - 1}{(x + 1) (x - 1)} = \lim_{x \to {(- 1)}^{+}} (\frac{1}{x + 1} . \frac{5 x^{2} - 4 x - 1}{x - 1})$

Mà: $\{\begin{cases} \lim_{x \to {(- 1)}^{+}} \frac{1}{x + 1} = + \infty \\ \lim_{x \to {(- 1)}^{+}} \frac{5 x^{2} - 4 x - 1}{x - 1} = - 4 < 0 \end{cases}$ nên $\lim_{x \to {(- 1)}^{+}} y = - \infty$ .

$\lim_{x \to {(- 1)}^{-}} y = \lim_{x \to {(- 1)}^{-}} \frac{5 x^{2} - 4 x - 1}{x^{2} - 1} = \lim_{x \to {(- 1)}^{-}} \frac{5 x^{2} - 4 x - 1}{(x + 1) (x - 1)} = \lim_{x \to {(- 1)}^{-}} (\frac{1}{x + 1} . \frac{5 x^{2} - 4 x - 1}{x - 1})$

Mà: $\{\begin{cases} \lim_{x \to {(- 1)}^{-}} \frac{1}{x + 1} = - \infty \\ \lim_{x \to {(- 1)}^{-}} \frac{5 x^{2} - 4 x - 1}{x - 1} = - 4 < 0 \end{cases}$ nên $\lim_{x \to {(- 1)}^{-}} y = + \infty$ .

Do đó, đồ thị hàm số có một tiệm cận đứng x=-1 .

Tổng cộng đồ thị hàm số có 2 tiệm cận.

Câu 2

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi trong các số có tất cả bao nhiêu số dương?

A. 1

B. 2

C. 0

D. 3

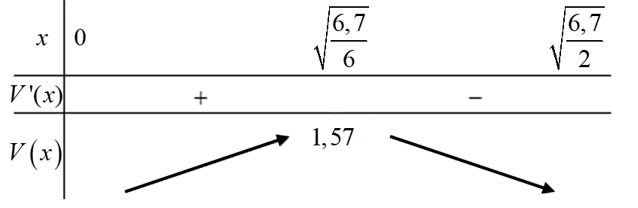
Lời giải

Chọn B

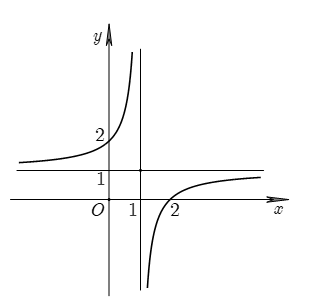
Nhìn vào đồ thị ta thấy

· Tiệm cận ngang của đồ thị hàm số là $y = \frac{a}{c}$ nằm phía trên trục hoành nên $\frac{a}{c} > 0 \Rightarrow a, c$ cùng dấu.

· Tiệm cận đứng của đồ thị hàm số là $x = \frac{- d}{c}$ nằm bên trái trục tung nên $\frac{- d}{c} < 0 \Rightarrow \frac{d}{c} > 0 \Rightarrow d, c$ cùng dấu.

· Giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên $\frac{b}{d} < 0$ $\Rightarrow b, d$ trái dấu.

Mà $a > 0 \Rightarrow c > 0, d > 0, b < 0$ .

Câu 3

a) Ông An dự định sử dụng hết 6,7 $m^{2}$ kính để làm một bể bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Hỏi bể có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho khối chóp tứ giác đều có cạnh đáy bằng 2a cạnh bên bằng a $\sqrt{5}$ . Thể tích của khối chóp đã cho bằng

A. $4 \sqrt{5} a^{3}$

B. $4 \sqrt{3} a^{3}$

C. $\frac{4 \sqrt{5} a^{3}}{3}$

D. $\frac{4 \sqrt{3} a^{3}}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị như hình vẽ bên dưới.

Tâm đối xứng của đồ thị hàm số có tọa độ là

A. $(- 1; 1)$

B. $(1; 2)$

C. $(1; 1)$

D. $(2; 1)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số đã cho trên đoạn $[0; 2]$ là bao nhiêu

A. -1

B. -3

C. 1

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số $y = f (x) = \frac{x + m}{x + 1}$ ( m là tham số). Tìm tất cả các giá trị của tham số m thỏa mãn $max_{[0; 1]} |f (x)| + min_{[0; 1]} |f (x)| = 2$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hàm số y=f(x) có đạo hàm liên tục trên và bảng xét dấu đạo hàm như sau: Hỏi hàm số y=3f(−x4+4x2−6)+2x6−3x4−12x2 có tất cả bao nhiêu điểm cực tiểu?

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=5x2−4x−1x2−1 là

Cho hàm số y=ax+bcx+d có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi trong các số có tất cả bao nhiêu số dương?

Cho khối chóp tứ giác đều có cạnh đáy bằng 2a cạnh bên bằng a5. Thể tích của khối chóp đã cho bằng

Cho hàm số y=ax+bcx+d có đồ thị như hình vẽ bên dưới. Tâm đối xứng của đồ thị hàm số có tọa độ là

Cho hàm số y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số đã cho trên đoạn 0 ; 2 là bao nhiêu

Cho hàm số y=fx=x+mx+1 ( m là tham số). Tìm tất cả các giá trị của tham số m thỏa mãn max0;1fx+min0;1fx=2

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $y = f (x)$ có đạo hàm liên tục trên và bảng xét dấu đạo hàm như sau:

Hỏi hàm số $y = 3 f (- x^{4} + 4 x^{2} - 6) + 2 x^{6} - 3 x^{4} - 12 x^{2}$ có tất cả bao nhiêu điểm cực tiểu?

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{5 x^{2} - 4 x - 1}{x^{2} - 1}$ là

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi trong các số có tất cả bao nhiêu số dương?

Cho khối chóp tứ giác đều có cạnh đáy bằng 2a cạnh bên bằng a $\sqrt{5}$ . Thể tích của khối chóp đã cho bằng

Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị như hình vẽ bên dưới.

Tâm đối xứng của đồ thị hàm số có tọa độ là

Cho hàm số y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số đã cho trên đoạn $[0; 2]$ là bao nhiêu

Cho hàm số $y = f (x) = \frac{x + m}{x + 1}$ ( m là tham số). Tìm tất cả các giá trị của tham số m thỏa mãn $max_{[0; 1]} |f (x)| + min_{[0; 1]} |f (x)| = 2$