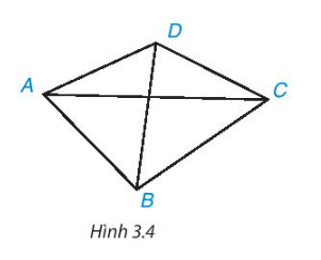
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
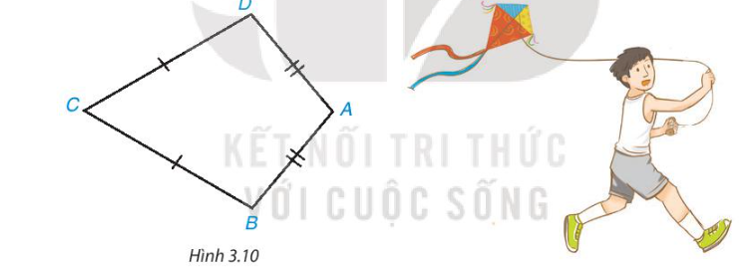
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
Câu hỏi trong đề: Giải SGK Toán 8 KNTT Bài 10. Tứ giác có đáp án !!
Quảng cáo
Trả lời:
a) Nối AC, BD (như hình vẽ
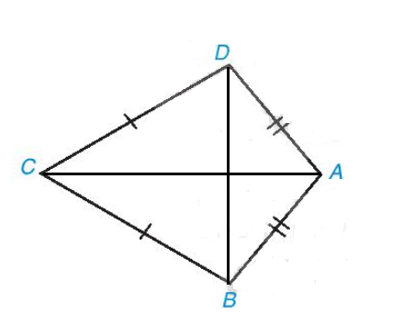
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
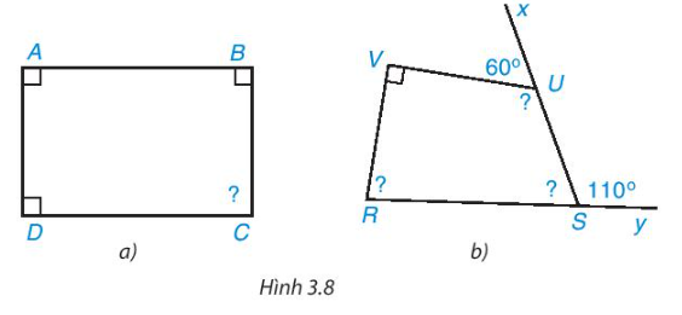
• Hình 3.8a)
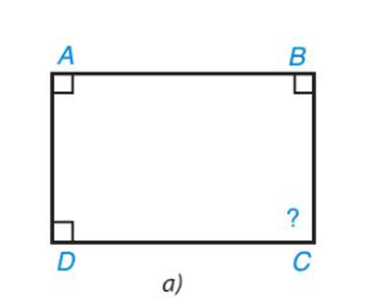
Xét tứ giác ABCD có: .
Hay .
Khi đó .
Do đó .
Vậy .
• Hình 3.8b)
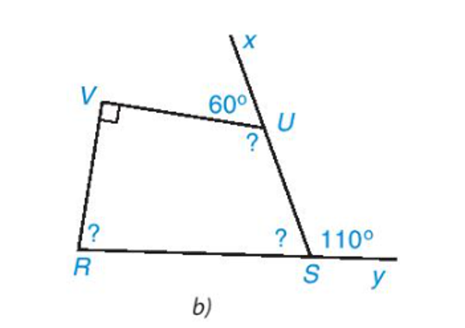
Vì và là hai góc kề bù nên ta có:
Hay .
Suy ra .
Vì và là hai góc kề bù nên ta có:
Hay .
Suy ra .
Do đó .
Xét tứ giác VUSR có: .
Hay
Khi đó
Do đó .
Vậy .
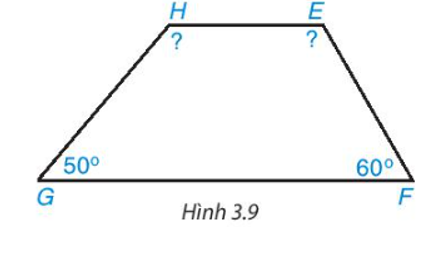
Lời giải
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
Suy ra .
Khi đó .
Suy ra .
Vậy ; .
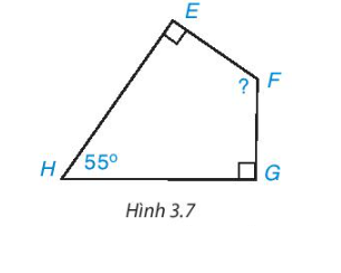
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Bảo nguyễn văn bảo
Sai từ trên xuống dưới