Câu hỏi:

12/07/2024 11,126

Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C.

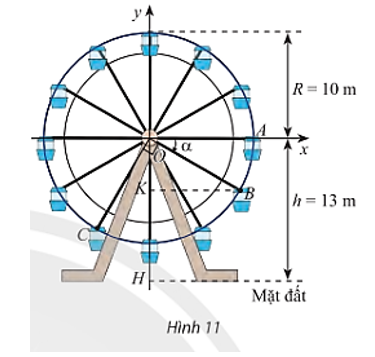
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sinα) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi α = – 30°.

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 11 CTST Bài 2: Giá trị lượng giác của một góc lượng giác có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Ta có điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là α trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm B(10cosα; 10sinα).

Vì vậy chiều cao từ điểm B đến mặt đất là: 13 + 10sinα (mét).

Với α = – 30° ta có chiều cao từ điểm B đến mặt đất là: 13 + 10sin.(– 30°) = 8 (mét).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được $3 \frac{1}{10}$ vòng là bao nhiêu, biết độ dài thanh OM là 15 cm? Kết quả làm tròn đến hàng phần mười.

Xem đáp án

Lời giải

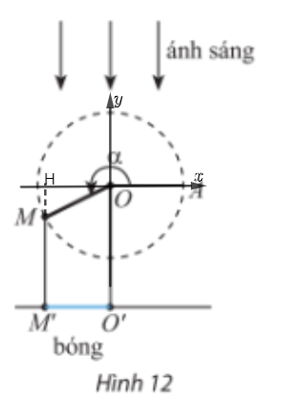
Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được (ảnh 2)

Kẻ MH vuông góc với Ox.

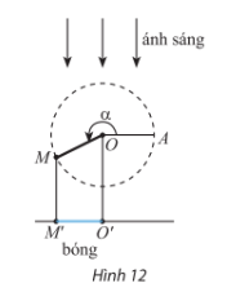
Điểm M là điểm biểu diễn góc lượng giác α

Ta có: $α = 3 \frac{1}{10} .360 ° = 1 116 °$

Khi đó M(cos1116°.15; sin1116°.15)

Suy ra OH = |cos1116°|.15 ≈12,1.

Vậy độ dài bóng O’M’ của OM khi thanh quay được $3 \frac{1}{10}$ vòng là 12,1 cm.

Câu 2

Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{π}{4}$ hoặc từ 0 đến 45° và tính:

a) $cos \frac{21 π}{6}$ ;

b) $sin \frac{129 π}{4}$ ;

c) tan1 020°.

Xem đáp án

Lời giải

a) Ta có: $cos \frac{21 π}{6} = cos (\frac{24 π}{6} - \frac{π}{2}) = cos (- \frac{π}{2}) = cos \frac{π}{2} = \sin 0$ .

b) $sin \frac{129 π}{4} = sin (32 π + \frac{π}{4}) = sin \frac{π}{4}$ .

c) tan1 020° = tan(3.180° – 60°) = tan(180° – 60°) = – tan60° = – cot30°.

Câu 3

Tính các giá trị lượng giác của góc α, nếu:

a) $\sin α = \frac{5}{13}$ và $\frac{π}{2} < α < π$ ;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển , khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dàu của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Rút gọn các biểu thức sau:

a) $\frac{1}{\tan α + 1} + \frac{1}{\cot α + 1}$ ;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho sinα = $\frac{12}{13}$ và cosα = $- \frac{5}{13}$ . Tính $\sin (- \frac{15 π}{2} - α) - cos (13 π + α)$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến π4 hoặc từ 0 đến 45° và tính: a) cos21π6; b) sin129π4; c) tan1 020°.

Tính các giá trị lượng giác của góc α, nếu: a) sinα=513 và π2<α<π;

Rút gọn các biểu thức sau: a) 1tanα+1+1cotα+1;

Cho sinα = 1213 và cosα = −513. Tính sin−15π2−α−cos13π+α.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{π}{4}$ hoặc từ 0 đến 45° và tính:

a) $cos \frac{21 π}{6}$ ;

b) $sin \frac{129 π}{4}$ ;

c) tan1 020°.

Tính các giá trị lượng giác của góc α, nếu:

a) $\sin α = \frac{5}{13}$ và $\frac{π}{2} < α < π$ ;

Rút gọn các biểu thức sau:

a) $\frac{1}{\tan α + 1} + \frac{1}{\cot α + 1}$ ;

Cho sinα = $\frac{12}{13}$ và cosα = $- \frac{5}{13}$ . Tính $\sin (- \frac{15 π}{2} - α) - cos (13 π + α)$ .