Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC.
Chứng minh tứ giác DEFG là một hình vuông.
Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC.
Chứng minh tứ giác DEFG là một hình vuông.
Quảng cáo
Trả lời:
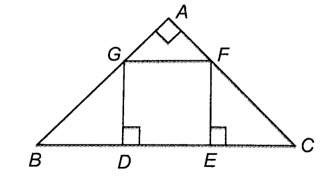
Do ∆ABC vuông cân tại A nên .
Xét ∆GBD vuông tại D và ∆EFC vuông tại E có:
BD = EC;
Do đó ∆GBD = ∆FCE (cạnh góc vuông – góc nhọn kề)
Suy ra
Mà nên
Do đó
Suy ra ∆GBD vuông cân tại D và ∆EFC vuông cân tại E.
Vì vậy GD = BD, EF = EC.
Mà
Suy ra GD = DE = EF.
Do GD ⊥ BC, EF ⊥ BC nên GD // EF
Tứ giác GDEF có GD // EF, GD = EF nên GDEF là hình chữ nhật.
Lại có GD và DE là hai cạnh kề của hình chữ nhật GDEF bằng nhau nên GDEF là hình vuông.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
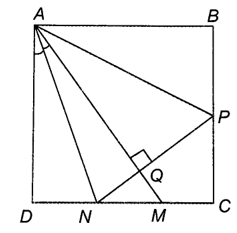
Đường thẳng NP ⊥ AM cắt AM ở Q.
Do ABCD là hình vuông nên ND ⊥ AD.
Xét DADN vuông tại D và DAQN vuông tại Q có:
AN là cạnh chung, (do AN là tia phân giác của )
Do đó ∆ADN = ∆AQN (cạnh huyền – góc nhọn)
Suy ra AD = AQ;
Mà AD = AB nên AQ = AB
Xét DAQP vuông tại Q và DABP vuông tại B có:
Cạnh AP chung; AQ = AB
Do đó ∆AQP = ∆ABP (cạnh huyền – cạnh góc vuông)
Suy ra .
Ta có:
Mà nên ta có:
Suy ra
Lời giải
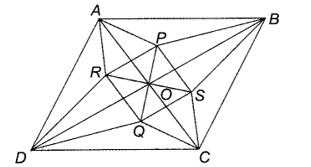
Gọi P, Q lần lượt là giao điểm ba đường phân giác của tam giác OAB, OCD thì O, P, Q thẳng hàng trên đường phân giác của góc AOB .
Do ABCD là hình bình hành nên AB // CD, AD // BC
Suy ra (các cặp góc ở vị trí so le trong)
Mà DQ, BP lần lượt là tia phân giác của nên
Xét ∆OBP và ∆ODQ có:
; OB = OD; (đối đỉnh)
Do đó ∆OBP = ∆ODQ (g.c.g)
Suy ra OP = OQ, hay O là trung điểm của PQ
Gọi R, S lần lượt là giao điểm ba đường phân giác của tam giác OAD, OBC thì tương tự như trên, ta cũng chứng minh được O là trung điểm của RS và đường thẳng RS là đường phân giác của góc
Do góc AOB và góc AOD là hai góc kề bù nên hai đường phân giác PQ, RS vuông góc với nhau.
Tứ giác PSQR có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau nên là hình thoi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.