Câu hỏi:

13/07/2024 2,611

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO.

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Chứng minh tứ giác ANCQ là hình bình hành.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 CTST Bài tập cuối chương 3 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

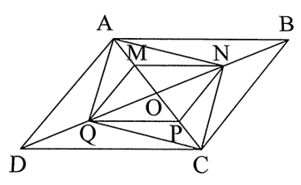
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO. a) Chứng minh tứ giác MNPQ là hình bình hành. b) Chứng minh tứ giác ANCQ là hình bình hành. (ảnh 1)

a) Xét ∆AOB có M, N lần lượt là trung điểm của AO, BO.

Theo bài 4, trang 63, SBT Toán 8 Tập Một, ta có: MN // AB; $MN = \frac{1}{2} AB.$ (1)

Tương tự, xét ∆OCD ta cũng có PQ // CD; $QP = \frac{1}{2} DC.$ (2)

Mà AB // CD; AB = CD (do ABCD là hình bình hành). (3)

Từ (1), (2) và (3) suy ra MN // PQ, MN = PQ.

Vậy tứ giác MNPQ là hình bình hành.

b) Xét ∆ANB và ∆CQD có:

AB = CD (ABCD là hình bình hành);

$\hat{ABN} = \hat{CDQ}$ (hai góc so le trong do AB // CD);

$BN = DQ (= \frac{1}{4} BD)$ (vì OB = OD, NO = NB, QO = QD)

Do đó ∆ANB = ∆CQD (c.g.c). Suy ra AN = CQ. (4)

Xét ∆AQD và ∆CNB có:

AD = BC (do ABCD là hình bình hành);

$\hat{ADQ} = \hat{CBN}$ (hai góc so le trong do AD // BC);

$DQ = BN (= \frac{1}{4} BD)$ .

Do đó ∆AQD = ∆CNB (c.g.c). Suy ra AQ = CN. (5)

Từ (4) và (5) suy ra ANCQ là hình bình hành.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh:

a) AIKD và BIKC là hình vuông.

b) $IK = \frac{DC}{2}$ và $\hat{DIC} = 90 ° .$

Xem đáp án

Lời giải

Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh: (ảnh 1)

Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh: (ảnh 2)

Câu 2

Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc $\hat{ADB}, \hat{DBC}$ (E ∈ AB, K ∈ CD).

a) Chứng minh DE // BK.

b) Giả sử DE ⊥ AB. Chứng minh DA = DB.

c) Trong trường hợp DE ⊥ AB, tìm số đo của $\hat{ADB}$ để tứ giác DEBK là hình vuông.

Xem đáp án

Lời giải

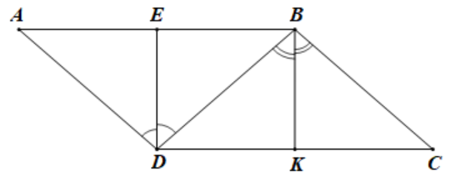
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc ADB, DBC (E ∈ AB, K ∈ CD). a) Chứng minh DE // BK. b) Giả sử DE ⊥ AB. Chứng minh DA = DB. c) Trong trường hợp DE ⊥ AB, tìm số đo của để tứ giác DEBK là hình vuông. (ảnh 1)

a) Ta có ABCD là hình bình hành nên AD // BC.

Suy ra $\hat{ADB} = \hat{DBC}$ (hai góc so le trong).

Do đó $\frac{\hat{ADB}}{2} = \frac{\hat{DBC}}{2}$

Suy ra $\hat{EDB} = \hat{KBD}$ (do DE, BK lần lượt là đường phân giác của $\hat{ADB}$ và $\hat{DBC}$ )

Mà hai góc này ở vị trí so le trong nên DE // BK.

Vậy DE // BK.

b) Xét ∆DAB có DE vừa là đường cao vừa là đường phân giác, suy ra ∆DAB cân tại D.

Khi đó, DA = DB.

c) Xét tứ giác DEBK có: DE // BK, BE // DK.

Suy ra DEBK là hình bình hành.

Mà $\hat{E} = 90 °$ nên DEBK là hình chữ nhật.

Để tứ giác DEBK là hình vuông thì DE = EB.

Mà ∆DAB cân tại D nên DE vừa là đường cao vừa là trung tuyến của ∆DAB.

Suy ra $DE = EB = \frac{AB}{2},$ suy ra ∆DAB vuông tại D hay $\hat{ADB} = 90 ° .$

Câu 3