Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72 cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1 m thì có thể đặt chiếc tivi mới vào đó không?
Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72 cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1 m thì có thể đặt chiếc tivi mới vào đó không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
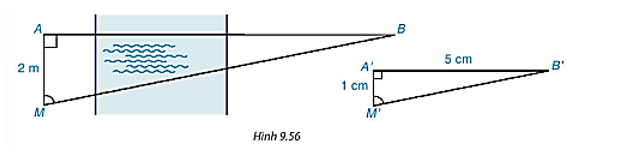
- Gọi chiều ngang của chiếc ti vi mới là x (m).
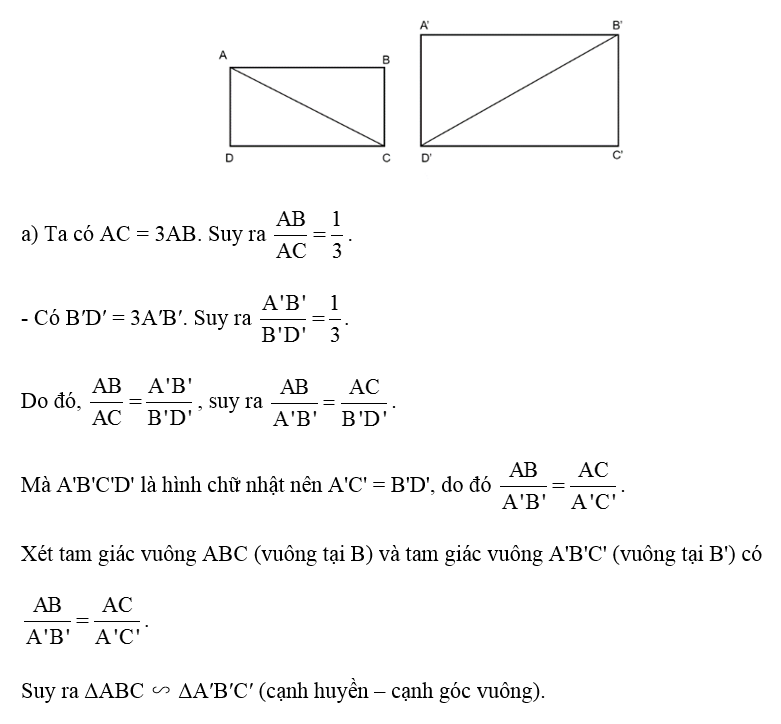
Xét hai tam giác vuông lần lượt có các cạnh góc vuông là hai cạnh (nằm ngang và thẳng đứng) của màn hình hai chiếc tivi 32 inch và 55 inch. Đường chéo của chúng có độ dài lần lượt là 32 inch và 55 inch. Hai tam giác vuông này đồng dạng với nhau vì có hai cặp cạnh góc vuông tỉ lệ. Do đó cm = 1,2375 m > 1 m.
Vậy không thể đặt vừa chiếc ti vi 55 inch vào khoảng trống hình vuông cạnh 1 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
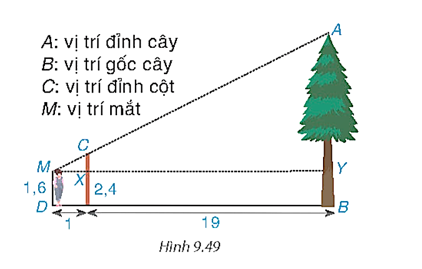
Ta có CX = 2,4 – 1,6 = 0,8 (m).
MY = 1 + 19 = 20 (m).
Xét tam giác MXC và tam giác MYA có:
chung
Do đó: ∆MXC ∽ ∆MYA (g.g).
Suy ra . Do đó, (m).
Vậy chiều cao của cây là AB = AY + YB = AY + MD = 16 + 1,6 = 17,6 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập