Một mảnh vườn hình chữ nhật có chiều rộng ngắn hơn chiều dài 6 m và có diện tích là 280 m2. Tính các kích thước của mảnh vườn đó.
Một mảnh vườn hình chữ nhật có chiều rộng ngắn hơn chiều dài 6 m và có diện tích là 280 m2. Tính các kích thước của mảnh vườn đó.
Quảng cáo
Trả lời:
Gọi chiều rộng mảnh vườn hình chữ nhật là x (m) (x > 0).
Chiều rộng ngắn hơn chiều dài 6 m nên chiều dài mảnh vườn là x + 6 (m).
Diện tích mảnh vườn là: x(x + 6) (m2).
Theo bài, mảnh vườn có diện tích là 280 m2 nên ta có phương trình:
x(x + 6) = 280.
x2 + 6x – 280 = 0.
Ta có ∆’ = 32 – 1.(–280) = 289 > 0 và ![]()
Do đó, phương trình có hai nghiệm phân biệt:
x1 = –3 + 17 = 14, x2 = –3 – 17 = –20.
Ta thấy chỉ có giá trị x1 = 14 thỏa mãn điều kiện x > 0.
Vậy chiều rộng mảnh vườn là 14 m và chiều dài mảnh vườn là 14 + 6 = 20 (m).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có ∆ = (–1)2 – 4.1.1 = –3 < 0.
Do đó, phương trình vô nghiệm.
Lời giải
Sau bài học này, chúng ta sẽ giải được bài toán trên như sau:
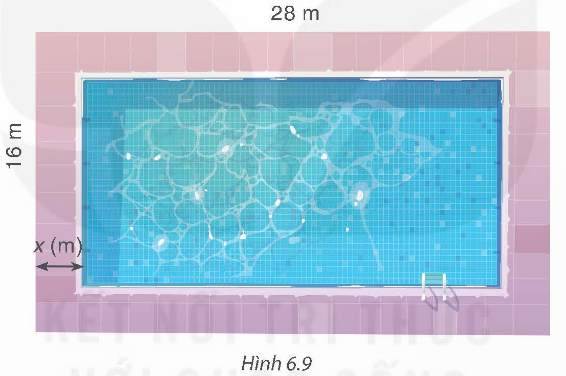
Theo bài, ta có điều kiện của x là 0 < x < 8.
Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).
Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).
Diện tích của bể bơi theo x là:
S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x2 = 4x2 – 88x + 448 (m2).
Theo bài, S = 288 m2 nên ta có phương trình: 4x2 – 88x + 448 = 288.
Giải phương trình:
4x2 – 88x + 448 = 288
4x2 – 88x + 160 = 0
x2 – 22x + 40 = 0.
Phương trình trên có a = 1; b’ = –11; c = 40 và ∆’ = (–11)2 – 1.40 = 81 nên ![]()
Do đó, phương trình trên có hai nghiệm phân biệt 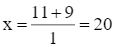 và
và 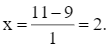
Ta thấy chỉ có x = 2 thỏa mãn điều kiện 0 < x < 16.
Vậy bề rộng của đường đi là 2 mét để diện tích của bể bơi là 288 m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.