Gọi x1, x2 là hai nghiệm của phương trình bậc hai x2 – 5x + 3 = 0. Không giải phương trình, hãy tính:
a)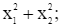 
b) (x1 – x2)2.
Gọi x1, x2 là hai nghiệm của phương trình bậc hai x2 – 5x + 3 = 0. Không giải phương trình, hãy tính:
a)
b) (x1 – x2)2.
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Luyện tập chung trang 28 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét phương trình bậc hai x2 – 5x + 3 = 0 có ∆ = (–5)2 – 4.1.3 = 13 > 0 nên phương trình có hai nghiệm phân biệt x1, x2.
Theo định lí Viète ta có:
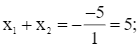
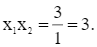
a) Ta có: 
Suy ra 
b) Ta có: 
Chú ý: Ta cũng có thể tính giá trị của (x1 – x2)2 như sau:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đổi 120 triệu đồng = 120 000 nghìn đồng.
Vì doanh thu đạt 120 triệu đồng nên R = 120 000 (nghìn đồng).
Thay R = 120 000 vào R = xp = x(100 – 0,02x), ta được:
x(100 – 0,02x) = 120 000
100x – 0,02x2 = 120 000
0,02x2 – 100x + 120 000 = 0.
Ta có ∆’ = (–50)2 – 0,02.120 000 = 100 > 0 và 
Suy ra phương trình có hai nghiệm phân biệt:
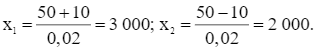
Vậy phải bán 3 000 chiếc áo với giá 100 – 0,02.3 000 = 40 nghìn đồng hoặc bán 2 000 chiếc áo với giá 100 – 0,02.2 000 = 60 nghìn đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x (cm) là độ dài cạnh đáy (x > 0).
Diện tích mặt đáy hình vuông là: x2 (cm2).
Diện tích xung quanh là: 4x . 10 = 40x (cm2).
Tổng diện tích xung quanh và diện tích đáy là: x2 + 40x (cm2).
Theo bài, tổng diện tích xung quanh và diện tích đáy là 800 cm2 nên ta có phương trình:
x2 + 40x = 800
x2 + 40x – 800 = 0.
Ta có: ∆’ = 202 – 1.(–800) = 1 200 > 0 và 
Suy ra phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện);
(loại).
Vậy độ dài cạnh đáy của chiếc hộp khoảng 14,64 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập