Câu hỏi:
13/07/2024 2,253
Nhu cầu của khách hàng đối với một loại áo phông tại một cửa hàng được cho bởi phương trình p = 100 – 0,02x, trong đó p là giá tiền của mỗi chiếc áo (nghìn đồng) và x là số lượng áo phông bán được. Doanh thu R (nghìn đồng) khi bán được x chiếc áo phông là:
R = xp = x(100 – 0,02x).
Hỏi cần phải bán được bao nhiêu chiếc áo phông để doanh thu đạt 120 triệu đồng?
Nhu cầu của khách hàng đối với một loại áo phông tại một cửa hàng được cho bởi phương trình p = 100 – 0,02x, trong đó p là giá tiền của mỗi chiếc áo (nghìn đồng) và x là số lượng áo phông bán được. Doanh thu R (nghìn đồng) khi bán được x chiếc áo phông là:
R = xp = x(100 – 0,02x).
Hỏi cần phải bán được bao nhiêu chiếc áo phông để doanh thu đạt 120 triệu đồng?
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Luyện tập chung trang 28 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đổi 120 triệu đồng = 120 000 nghìn đồng.
Vì doanh thu đạt 120 triệu đồng nên R = 120 000 (nghìn đồng).
Thay R = 120 000 vào R = xp = x(100 – 0,02x), ta được:
x(100 – 0,02x) = 120 000
100x – 0,02x2 = 120 000
0,02x2 – 100x + 120 000 = 0.
Ta có ∆’ = (–50)2 – 0,02.120 000 = 100 > 0 và 
Suy ra phương trình có hai nghiệm phân biệt:
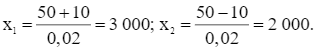
Vậy phải bán 3 000 chiếc áo với giá 100 – 0,02.3 000 = 40 nghìn đồng hoặc bán 2 000 chiếc áo với giá 100 – 0,02.2 000 = 60 nghìn đồng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (cm) là độ dài cạnh đáy (x > 0).
Diện tích mặt đáy hình vuông là: x2 (cm2).
Diện tích xung quanh là: 4x . 10 = 40x (cm2).
Tổng diện tích xung quanh và diện tích đáy là: x2 + 40x (cm2).
Theo bài, tổng diện tích xung quanh và diện tích đáy là 800 cm2 nên ta có phương trình:
x2 + 40x = 800
x2 + 40x – 800 = 0.
Ta có: ∆’ = 202 – 1.(–800) = 1 200 > 0 và 
Suy ra phương trình có hai nghiệm phân biệt:
(thỏa mãn điều kiện);
(loại).
Vậy độ dài cạnh đáy của chiếc hộp khoảng 14,64 cm.
Lời giải
Xét phương trình bậc hai x2 – 5x + 3 = 0 có ∆ = (–5)2 – 4.1.3 = 13 > 0 nên phương trình có hai nghiệm phân biệt x1, x2.
Theo định lí Viète ta có:
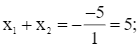
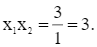
a) Ta có: 
Suy ra 
b) Ta có: 
Chú ý: Ta cũng có thể tính giá trị của (x1 – x2)2 như sau:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận