Câu hỏi:
24/08/2024 21,478
Một cổng vòm được thiết kế dạng parabol y = ax2 như hình dưới đây. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao cổng là OI = 4,5 m.
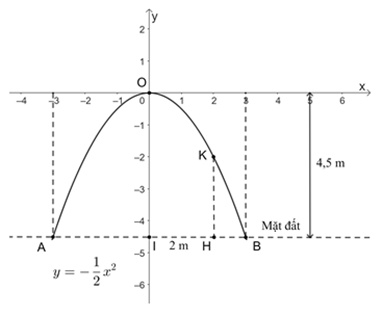
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2 m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể qua được cổng vòm đó hay không?
Một cổng vòm được thiết kế dạng parabol y = ax2 như hình dưới đây. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao cổng là OI = 4,5 m.
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2 m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể qua được cổng vòm đó hay không?
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài 18. Hàm số y = ax^2 (a ≠ 0) có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì điểm (3; 4,5) thuộc parabol nên ta có: 4,5 = a.32, suy ra \(a = - \frac{1}{2}.\)
Từ đó ta có \(HK = \left| { - 4,5 - \left( { - \frac{1}{2}{{.2}^2}} \right)} \right| = \left| { - 4,5 + 2} \right| = 2,5\) (m).
b) Do xe tải có chiều rộng 2 m nên ta tính chiều cao cổng tại vị trí cách I là 1 m, tương ứng với x = 1. Tại x = 1, chiều cao cổng là \(\left| { - 4,5 - \left( { - \frac{1}{2}{{.1}^2}} \right)} \right| = 4\) (m). Do chiều cao cổng tại vị trí này lớn hơn chiều cao của xe tải nên xe tải có thể qua được cổng vòm.
Nhà sách vietjack
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết rằng đường cong trong hình bên là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = −2.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
Biết rằng đường cong trong hình bên là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = −2.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
Xem đáp án »
24/08/2024
9,017
Câu 2:
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.
a) Viết công thức tính thể tích V của hình lăng trụ theo a và tính giá trị của V khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10 cm.
a) Viết công thức tính thể tích V của hình lăng trụ theo a và tính giá trị của V khi a = 2 cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Xem đáp án »
24/08/2024
8,744
Câu 3:
Diện tích toàn phần S (cm2) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy, là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm2.
Diện tích toàn phần S (cm2) của hình lập phương, tức là tổng diện tích xung quanh và diện tích của hai mặt đáy, là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 cm2.
Xem đáp án »
24/08/2024
7,341
Câu 4:
Vẽ đồ thị của các hàm số sau:
a) y = 3x2;
b) \(y = - \frac{1}{3}{x^2}.\)
Vẽ đồ thị của các hàm số sau:
a) y = 3x2;
b) \(y = - \frac{1}{3}{x^2}.\)
Xem đáp án »
24/08/2024
6,003
Câu 5:
Cho hàm số y = 0,25x2. Hoàn thành bảng giá trị sau vào vở:
x
−3
−2
−1
0
1
2
3
y
?
?
?
?
?
?
?
Cho hàm số y = 0,25x2. Hoàn thành bảng giá trị sau vào vở:
|
x |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
|
y |
? |
? |
? |
? |
? |
? |
? |
Xem đáp án »
24/08/2024
1,966
Câu 6:
Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là F = av2 (a là hằng số). Biết rằng khi tốc độ gió bằng 3 m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 270 N.
a) Tính hằng số a.
b) Hỏi khi tốc độ gió v = 10 m/s thì lực thổi F của gió bằng bao nhiêu?
c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 10 000 N, hỏi chiếc thuyền đó có thể đi được trong gió bão với tốc độ gió 72 km/h không?
Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là F = av2 (a là hằng số). Biết rằng khi tốc độ gió bằng 3 m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 270 N.
a) Tính hằng số a.
b) Hỏi khi tốc độ gió v = 10 m/s thì lực thổi F của gió bằng bao nhiêu?
c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 10 000 N, hỏi chiếc thuyền đó có thể đi được trong gió bão với tốc độ gió 72 km/h không?
Xem đáp án »
24/08/2024
1,453
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận