Câu hỏi:
24/08/2024 7,707
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \[\widehat {BOC} = 120^\circ \] và \[\widehat {OCA} = 20^\circ .\] Tính số đo các góc của tam giác ABC.
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \[\widehat {BOC} = 120^\circ \] và \[\widehat {OCA} = 20^\circ .\] Tính số đo các góc của tam giác ABC.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung trang 78 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
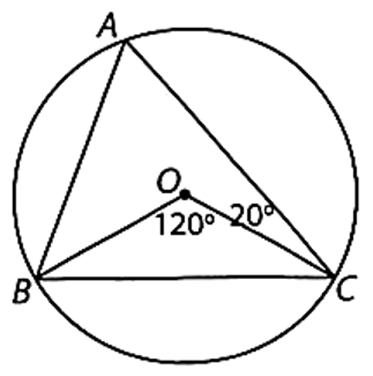
Ta có \(\widehat A = \frac{{\widehat {BOC}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \) (góc nội tiếp \(\widehat A\) và góc ở tâm \[\widehat {BOC}\] cùng chắn cung ).
Tam giác AOC cân tại O nên \[\widehat {AOC} = 180^\circ - \widehat {OAC} - \widehat {OCA} = 180^\circ - 2\widehat {OCA} = 140^\circ .\]
Suy ra \[\widehat B = \frac{{\widehat {AOC}}}{2} = \frac{{140^\circ }}{2} = 70^\circ .\]
Do tổng các góc trong ∆ABC bằng 180° nên \(\widehat C = 180^\circ - \widehat A - \widehat B = 50^\circ .\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \(R = \frac{{\sqrt 3 }}{3}.3 = \sqrt 3 \) (cm).
b) Bán kính đường tròn nội tiếp của tam giác ABC là: \(r = \frac{{\sqrt 3 }}{6}.3 = \frac{{\sqrt 3 }}{2}\) (cm).
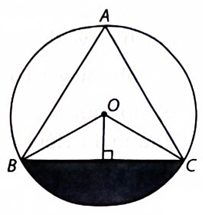
Chiều cao từ đỉnh O xuống cạnh BC của ∆OBC bằng bán kính đường tròn nội tiếp của tam giác ABC. Do vậy
\({S_{OBC}} = \frac{1}{2}r.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\) (cm2).
Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2.60^\circ = 120^\circ .\) Diện tích hình quạt chắn cung nhỏ BC là:
\(S' = \frac{{120}}{{360}}\pi .{\left( {\sqrt 3 } \right)^2} = \pi \) (cm2).
Vậy diện tích hình viên phân cần tính là:
\(S = S' - {S_{OBC}} = \pi - \frac{{3\sqrt 3 }}{4} \approx 1,84\) (cm2).
Lời giải
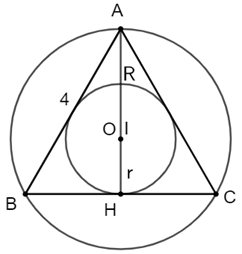
Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác đều ABC. Ta có \(R = \frac{{\sqrt 3 }}{3}.4 = \frac{{4\sqrt 3 }}{3}\) (cm), \(r = \frac{{\sqrt 3 }}{6}.4 = \frac{{2\sqrt 3 }}{3}\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận