Câu hỏi:
24/08/2024 6,817
Trong một khu vui chơi có dạng hình tam giác đều với độ dài cạnh bằng 60 m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa là 50 m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Trong một khu vui chơi có dạng hình tam giác đều với độ dài cạnh bằng 60 m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa là 50 m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung trang 78 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
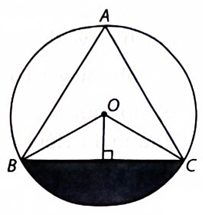
Giả sử khu vui chơi có dạng tam giác đều ABC. Gọi O là tâm đường tròn ngoại tiếp và R là bán kính của đường tròn ngoại tiếp tam giác ABC. Khi đó ta có
\(R = \frac{{\sqrt 3 }}{3}.60 = 20\sqrt 3 \) (cm).
Do R < 50 nên lắp đặt bộ phát sóng wifi vào vị trí O thì cả hình tròn tâm O bán kính R đều nằm trong vùng phủ sóng. Vì mọi điểm trong khu vui chơi đều không nằm ngoài diện tích của đường tròn (O; R) nên đều có thể bắt được sóng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
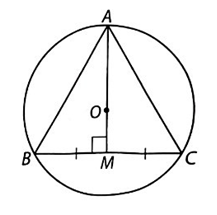
a) Ta có \(R = \frac{{\sqrt 3 }}{3}.3 = \sqrt 3 \) (cm).
b) Bán kính đường tròn nội tiếp của tam giác ABC là: \(r = \frac{{\sqrt 3 }}{6}.3 = \frac{{\sqrt 3 }}{2}\) (cm).
Chiều cao từ đỉnh O xuống cạnh BC của ∆OBC bằng bán kính đường tròn nội tiếp của tam giác ABC. Do vậy
\({S_{OBC}} = \frac{1}{2}r.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\) (cm2).
Ta có \(\widehat {BOC} = 2\widehat {BAC} = 2.60^\circ = 120^\circ .\) Diện tích hình quạt chắn cung nhỏ BC là:
\(S' = \frac{{120}}{{360}}\pi .{\left( {\sqrt 3 } \right)^2} = \pi \) (cm2).
Vậy diện tích hình viên phân cần tính là:
\(S = S' - {S_{OBC}} = \pi - \frac{{3\sqrt 3 }}{4} \approx 1,84\) (cm2).
Lời giải
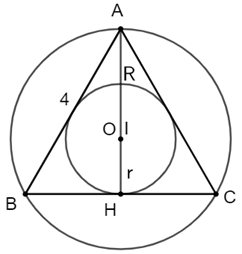
Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác đều ABC. Ta có \(R = \frac{{\sqrt 3 }}{3}.4 = \frac{{4\sqrt 3 }}{3}\) (cm), \(r = \frac{{\sqrt 3 }}{6}.4 = \frac{{2\sqrt 3 }}{3}\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận