Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian. Liên hệ giữa quãng đường chuyển động s (mét) và thời gian chuyển động x (giây) được cho bởi hàm số s = 4,9x2. Người ta thả một vật nặng từ độ cao 56 m trên tháp nghiêng Pi–sa xuống đất (sức cản của không khí không đáng kể).
a) Hỏi sau thời gian 2,5 giây vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất 17,584 m thì nó đã rơi thời gian bao nhiêu giây?
Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian. Liên hệ giữa quãng đường chuyển động s (mét) và thời gian chuyển động x (giây) được cho bởi hàm số s = 4,9x2. Người ta thả một vật nặng từ độ cao 56 m trên tháp nghiêng Pi–sa xuống đất (sức cản của không khí không đáng kể).
a) Hỏi sau thời gian 2,5 giây vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất 17,584 m thì nó đã rơi thời gian bao nhiêu giây?
Quảng cáo
Trả lời:
a) Ta có công thức s = 4,9x2
Thay x = 2,5 giây vào công thức trên ta có: S = 4,9.2,52 = 30,625 (m).
Vậy sau thời gian 2,5 giây vật nặng còn cách mặt đất số mét là:
56 ‒ 30,625 = 25,375 (m).
b) Quãng đường vật nặng đi được khi vật nặng còn cách mặt đất 17,584 m là:
56 – 17,584 = 38,416 (m).
Thời gian vật nặng đi được quãng đường 38,416 m là \(\sqrt {\frac{{38,416}}{{4,9}}} = 2,8\) (giây).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
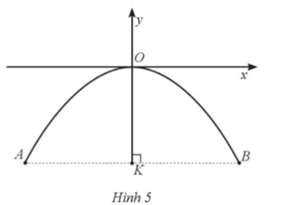
Từ Hình 5, ta có K(0; –4,5).
Gọi hoành độ của điểm B là b (b > 0).
Do tung độ của điểm B bằng tung độ của K nên B(b; –4,5).
Mặt khác, B thuộc parabol \(y = - \frac{1}{8}{x^2}\) nên ta có:
\( - 4,5 = - \frac{1}{8}{b^2}\) hay b2 = 36, nên b = 6 (do b > 0).
Từ đó KB = 6 m và AB = 2.KB = 2.6 = 12 m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất bằng 12 mét.
Lời giải
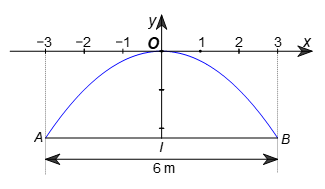
Gọi I là trung điểm của đoạn AB. Khi đó OI = h và \(AI = IB = \frac{{AB}}{2} = \frac{6}{2} = 3\,\,\left( {\rm{m}} \right).\)
Từ đó, trong hệ trục Oxy, hoành độ của B bằng 3, tung độ của B bằng –h.
Do đó: \( - h = - \frac{1}{4} \cdot {3^2}\) hay \( - h = \frac{{ - 9}}{4},\) suy ra \(h = \frac{9}{4} = 2,25\,\,\left( {\rm{m}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.