Câu hỏi:
28/08/2024 2,135
Cho hàm số \(y = - \frac{{{x^2}}}{2}.\)
a) Vẽ đồ thị của hàm số.
b) Đường thẳng y = ax + b cắt đồ thị của hàm số đã cho tại hai điểm A và B có hoành độ lần lượt bằng 1 và –2. Hãy xác định a và b.
Cho hàm số \(y = - \frac{{{x^2}}}{2}.\)
a) Vẽ đồ thị của hàm số.
b) Đường thẳng y = ax + b cắt đồ thị của hàm số đã cho tại hai điểm A và B có hoành độ lần lượt bằng 1 và –2. Hãy xác định a và b.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có bảng giá trị của hàm số:
|
x |
–4 |
–2 |
0 |
2 |
4 |
|
\(y = - \frac{{{x^2}}}{2}\) |
–8 |
–2 |
0 |
–2 |
–8 |
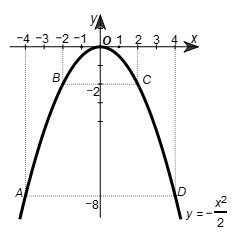
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒4; ‒8); B (‒2; ‒2); O(0; 0); C(2; ‒2); D(4; ‒8).
• Đồ thị của hàm số \(y = - \frac{{{x^2}}}{2}\) là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.
b) Do đường thẳng y = ax + b cắt đồ thị của hàm số đã cho tại hai điểm A và B có hoành độ lần lượt bằng 1 và – 2 nên xA = 1; xB = ‒2.
Thay toạ độ của điểm A(1; yA) vào \(y = - \frac{{{x^2}}}{2},\) ta được \({y_A} = - \frac{{{1^2}}}{2} = - \frac{1}{2}.\)
Do đó \(A\left( {1; - \frac{1}{2}} \right).\)
Thay toạ độ của điểm B(‒2; yB) vào \(y = - \frac{{{x^2}}}{2},\) ta được \({y_B} = - \frac{{{{\left( { - 2} \right)}^2}}}{2} = - \frac{4}{2} = - 2.\)
Do đó B(– 2; – 2).
Điểm \(A\left( {1; - \frac{1}{2}} \right)\) thuộc đường thẳng y = ax + b nên thay \(x = 1,\,\,y = - \frac{1}{2}\) vào hàm số y = ax + b, ta được: \( - \frac{1}{2} = a \cdot 1 + b\) hay \(a + b = - \frac{1}{2}.\) (1)
Điểm B(–2; –2) thuộc đường thẳng y = ax + b nên thay x = –2, y = –2 vào hàm số y = ax + b, ta được: –2 = a.(–2) + b hay – 2a + b = – 2. (2)
Từ (1) và (2), ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = - \frac{1}{2}}\\{ - 2a + b = - 2.}\end{array}} \right.\)
Trừ từng vế phương trình thứ nhất và phương trình thứ hai của hệ trên, ta được:
\(3a = \frac{3}{2},\) suy ra \(a = \frac{1}{2}.\)
Thay \(a = \frac{1}{2}\) vào phương trình \(a + b = - \frac{1}{2},\) ta được:
\(\frac{1}{2} + b = - \frac{1}{2},\) suy ra b = –1.
Vậy \(a = \frac{1}{2},\;\,\,b = - 1.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Do đồ thị (P) cắt đường thẳng d tại điểm B có hoành độ bằng 1 nên x = 1, thay vào hàm số y = –2x + 4, ta được y = ‒2.1 + 4 = ‒2 + 4 = 2.
Do đó B(1; 2).
Vì B(1; 2) cũng thuộc đồ thị (P): y = ax2, nên ta có:
2 = a.12, suy ra a = 2.
Vậy (P): y = 2x2.
Ta có bảng giá trị của hàm số:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = 2x2 |
8 |
2 |
0 |
2 |
8 |
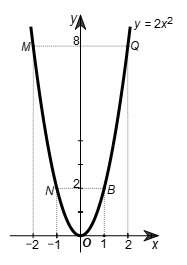
• Trên mặt phẳng tọa độ Oxy, lấy các điểm M(‒2; 8); N(‒1; 2); O(0; 0); B(1; 2); Q(2; 8).
• Đồ thị của hàm số y = 2x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.
b) Do đường thẳng d’: y = (m + 3)x – 2 cắt đồ thị (P) của hàm số tại điểm A có hoành độ bằng 4 nên x = 4
Thay x = 4 vào hàm số y = 2x2, ta được: y = 2.42 = 2.16 = 32.
Do đó A(4; 32).
Vì điểm A(4; 32) cũng thuộc d’ nên ta có:
32 = (m + 3).4 – 2
32 = 4m + 12 ‒ 2
4m = 22
\[m = \frac{{11}}{2}.\]
Vậy \[m = \frac{{11}}{2}\] thì đường thẳng d’: y = (m + 3)x – 2 cắt đồ thị (P) của hàm số tại điểm A có hoành độ bằng 4.
Lời giải
a) Với A(–3; 27) ta thay x = ‒3; y = 27 vào hàm số y = ax2 ta được:
27 = a.(‒3)2 hay 9a = 27, suy ra a = 3.
Vậy y = 3x2.
Ta có bảng giá trị của hàm số:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = 3x2 |
12 |
3 |
0 |
3 |
12 |
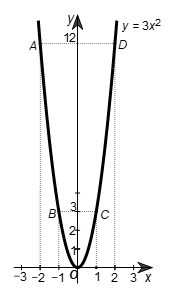
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒2; 12); B (‒1; 3); O(0; 0); C(1; 3); D(2; 12).
• Đồ thị của hàm số y = 3x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.
b) Với B(– 2; – 3) ta thay x = ‒2; y = ‒3 vào hàm số y = ax2 ta được:
‒3 = a.(‒2)2 hay 4a = ‒ 3, suy ra \(a = - \frac{3}{4}.\)
Vậy\(\;y = - \frac{3}{4}{x^2}\).
Ta có bảng giá trị của hàm số:
|
x |
– 2 |
– 1 |
0 |
1 |
2 |
|
\(y = - \frac{3}{4}{x^2}\) |
– 3 |
\( - \frac{3}{4}\) |
0 |
\( - \frac{3}{4}\) |
– 3 |
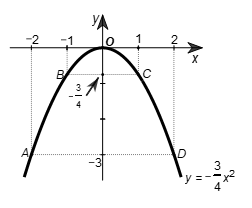
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒2; ‒3); \[B\left( { - 1; - \frac{3}{4}} \right);\] O(0; 0); \[C\left( {1; - \frac{3}{4}} \right);\] D(2; ‒3).
• Đồ thị của hàm số \(y = - \frac{3}{4}{x^2}\) là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1