Câu hỏi:
28/08/2024 4,568
Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax2 (a ≠ 0) đi qua điểm M(2; –2).
a) Tìm hệ số a, vẽ (P) với a vừa tìm được.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –3.
c) Tìm các điểm thuộc parabol có tung độ y = –4,5.
Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax2 (a ≠ 0) đi qua điểm M(2; –2).
a) Tìm hệ số a, vẽ (P) với a vừa tìm được.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –3.
c) Tìm các điểm thuộc parabol có tung độ y = –4,5.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đồ thị hàm số (P): y = ax2 đi qua điểm M(2; –2) nên thay x = 2; y = –2 vào hàm số y = ax2, ta được
‒2 = a.22 hay 4a = ‒2, suy ra \(a = - \frac{1}{2}.\)
Vậy \((P):y = - \frac{1}{2}{x^2}.\)
Ta có bảng giá trị của hàm số:
|
\(x\) |
–4 |
–2 |
0 |
2 |
4 |
|
\(y = - \frac{1}{2}{x^2}\) |
‒8 |
‒2 |
0 |
‒2 |
‒8 |
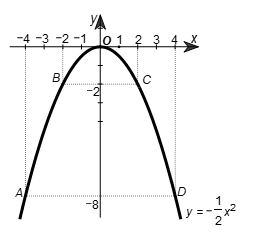
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒4; ‒8); B (‒2; ‒2); O(0; 0); C(2; ‒2); D(4; ‒8).
• Đồ thị của hàm số \(y = - \frac{{{x^2}}}{2}\) là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.
b) Thay x = –3 vào hàm số \(y = - \frac{1}{2}{x^2},\) ta được \[y = - \frac{1}{2} \cdot {\left( { - 3} \right)^2} = - \frac{9}{2}.\]
Vậy tung độ của điểm thuộc parabol có hoành độ x = –3 là bằng \( - \frac{9}{2}.\)
c) Thay y = –4,5 vào hàm số \(y = - \frac{1}{2}{x^2},\) ta được:
\( - 4,5 = - \frac{1}{2}{x^2},\) suy ra x2 = 9, do đó x = 3; x = –3.
Vậy các điểm (–3; –4,5) và (3; –4,5) thuộc parabol có tung độ y = –4,5.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét phương trình 5x2 – 7x + 1 = 0 có ∆ = (–7)2 – 4.5.1 = 49 – 20 = 29 > 0.
Do đó phương trình đã cho có hai nghiệm phân biệt.
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{ - 7}}{5} = \frac{7}{5};\,\,\,{x_1}{x_2} = \frac{1}{5}.\)
Ta có: \(A = \left( {{x_1} - \frac{7}{5}} \right){x_1} + \frac{1}{{25x_2^2}} + x_2^2\)
\( = \left[ {{x_1} - \left( {{x_1} + {x_2}} \right)} \right]{x_1} + {\left( {\frac{1}{5}} \right)^2} \cdot \frac{1}{{x_2^2}} + x_2^2\)
\( = \left[ {{x_1} - {x_1} - {x_2}} \right]{x_1} + {\left( {{x_1}{x_2}} \right)^2} \cdot \frac{1}{{x_2^2}} + x_2^2\)
\( = - {x_1}{x_2} + x_1^2x_2^2 \cdot \frac{1}{{x_2^2}} + x_2^2\)
\( = - {x_1}{x_2} + x_1^2 + x_2^2\)
\( = - {x_1}{x_2} + \left( {x_1^2 + x_2^2 + 2{x_1}{x_2}} \right) - 2{x_1}{x_2}\)
\( = - {x_1}{x_2} + {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\)
\( = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\)
\( = {\left( {\frac{7}{5}} \right)^2} - 3 \cdot \frac{1}{5} = \frac{{49}}{{25}} - \frac{3}{5} = \frac{{49}}{{25}} - \frac{{15}}{{25}} = \frac{{34}}{{25}}.\)
Lời giải
Gọi x là số sản phẩm mà người công nhân phải làm theo kế hoạch mỗi ngày (x ∈ ℕ*, x < 120).
Số sản phẩm mỗi ngày mà người đó đã làm theo thực tế là x + 3 (sản phẩm).
Thời gian mà người đó phải hoàn thành theo kế hoạch là \(\frac{{120}}{x}\) (ngày).
Thời gian mà người đó đã hoàn thành theo thực tế là \(\frac{{120}}{{x + 3}}\) (ngày).
Theo bài, người đó đã hoàn thành công việc sớm hơn dự định 2 ngày nên ta có phương trình: \(\frac{{120}}{x} - \frac{{120}}{{x + 3}} = 2.\)
Giải phương trình:
\(\frac{{120}}{x} - \frac{{120}}{{x + 3}} = 2\)
\(\frac{{60}}{x} - \frac{{60}}{{x + 3}} = 1\)
\(\frac{{60\left( {x + 3} \right)}}{{x\left( {x + 3} \right)}} - \frac{{60x}}{{x\left( {x + 3} \right)}} = \frac{{x\left( {x + 3} \right)}}{{x\left( {x + 3} \right)}}\)
60(x + 3) – 60x = x(x + 3)
60x + 180 – 60x = x2 + 3x
x2 + 3x ‒180 = 0
Phương trình trên có a = 1, b = 3, c = ‒180, ∆ = 32 ‒ 4.1.(‒180) = 9 + 720 = 729 > 0.
Do đó, phương trình có hai nghiệm phân biệt là
\[{x_1} = \frac{{ - 3 + \sqrt {729} }}{{2 \cdot 1}} = \frac{{ - 3 + 27}}{2} = \frac{{24}}{2} = 12;\]
\[{x_2} = \frac{{ - 3 - \sqrt {729} }}{{2 \cdot 1}} = \frac{{ - 3 - 27}}{2} = \frac{{ - 30}}{2} = - 15.\]
Ta thấy chỉ có giá trị x1 = 12 thoả mãn điều kiện.
Vậy theo kế hoạch, mỗi ngày công nhân đó phải làm 12 sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận