Câu hỏi:
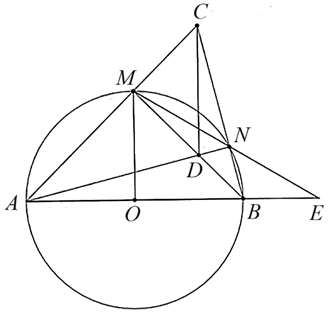
29/08/2024 96Cho đường tròn tâm \(O\) đường kính \[AB\] và \(M\) là điểm chính giữa của cung \[AB\]. Lấy điểm \(D\) thuộc dây \(MB\,\,\left( D \right.\) khác \(M\) và \(\left. B \right).\) Tia \[AD\] cắt cung nhỏ \[BM\] tại \(N,\) tia \[AM\] cắt tia \[BN\] tại \(C.\)
1) Chứng minh: tứ giác \(CMDN\) nội tiếp được đường tròn.
2) Chứng minh: \(AM \cdot AC = AD \cdot AN.\)
3) Chứng minh: \(\widehat {MCD} = \widehat {OMB}.\)
4) Gọi \[E\] là giao điểm của tia \[AB\] và tia \[MN.\] Chứng minh: \(\widehat {DBN} = \widehat {NEB}.\)
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Do \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) (các góc nội tiếp chắn nửa đường tròn) nên \(\widehat {CMB} = \widehat {CND} = 90^\circ .\)
Xét tứ giác \[CMDN\] có
\[\widehat {CMD} + \widehat {CND} = 90^\circ + 90^\circ = 180^\circ .\]
Mà hai góc này ở vị trí đối diện nên tứ giác \[CMDN\] nội tiếp được trong đường tròn.
2) Xét \(\Delta AMD\) và \(\Delta ANC\) có \(\widehat {NAC}\) chung; \(\widehat {AMD} = \widehat {ANC} = 90^\circ .\)
Do đó , suy ra \(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}}\) hay \(AM \cdot AC = AN \cdot AD\).
3) Do \[ABNM\] nội tiếp \(\left( O \right)\) nên \(\widehat {BAM} + \widehat {BNM} = 180^\circ \).
Mà \(\widehat {BNM} + \widehat {CNM} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CNM} = \widehat {BAM}\).
Mà \[\widehat {CNM} = \widehat {MCD}\] (góc nội tiếp cùng chắn cung
Suy ra \(\widehat {MCD} = \widehat {OMB}\,\,\left( { = \widehat {CNM}} \right)\) hay \(\widehat {MCD} = \widehat {OMB}.\)
4) Do \[M\] là điểm chính giữa cung \[AB\] nên \(MA = MB\).
Suy ra \(\widehat {MNA} = \widehat {MAB}\) (góc nội tiếp chắn hai cung bằng nhau).
Xét \(\Delta MAN\) và \(\Delta MAE\) có \(\widehat {AME}\) chung; \(\widehat {MNA} = \widehat {MAE}\,\,({\rm{cmt}})\).
Do đó .
Suy ra \(\widehat {MAN} = \widehat {MEA}\) (hai góc tương ứng).
Mà \[\widehat {MAN} = \widehat {MBN}\] (góc nội tiếp cùng chắn nên \(\widehat {MBN} = \widehat {MEB}\).
Do đó \(\widehat {DBN} = \widehat {NEB}\) (đpcm).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
Một khu vườn hình chữ nhật có chu vi \[200{\rm{ m}}.\] Do mở rộng đường giao thông nông thôn nên chiều dài khu vườn giảm \[8{\rm{ m}}.\] Tính chiều dài và chiều rộng của khu vườn ban đầu, biết diện tích đất còn lại để trồng cây là \(2\,080\;\,{{\rm{m}}^2}\).
Xem đáp án »
29/08/2024
196
Câu 2:
Cho Parabol \(\left( P \right):y = \frac{3}{4}{x^2}\) và đường thẳng \(\left( d \right):y = x + m\) với \(m\) là tham số.
1) Vẽ đồ thị của hàm số \(y = \frac{3}{4}{x^2}\).
2) Tìm điều kiện của tham số \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.
Xem đáp án »
29/08/2024
70
Câu 3:
1) Giải phương trình, hệ phương trình sau:
a) \({x^4} - 8{x^2} - 9 = 0\). b) \(\left\{ {\begin{array}{*{20}{l}}{x + y = 9}\\{3x - 2y = - 3}\end{array}} \right.\).
2) Rút gọn biểu thức sau: \(M = 2\sqrt {9 - 4\sqrt 5 } - \sqrt {20} .\)
Xem đáp án »
29/08/2024
49
Câu 4:
Cho phương trình: \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 8 = 0\). (\(m\) là tham số).
1) Tìm các giá trị của tham số \(m\) để phương trình đã cho có nghiệm bằng 2.
2) Tìm các giá trị của tham số \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện \(4{x_1} - 3{x_2} = 25\).
Xem đáp án »
29/08/2024
43
về câu hỏi!