Cho hình tứ diện OABC có G(3; −3; 6) là trọng tâm. Tìm tọa độ điểm A thỏa mãn \(\overrightarrow {AB} \) = (1; 2; 3) và \(\overrightarrow {AC} \) = (−1; 4; −2).

Hình chiếu của A(1; 2; 3) trên trục Oy là A'(0; 2; 0).

Khoảng cách từ A trên trục Oy là AA' = \(\sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {2 - 2} \right)}^2} + {{\left( {3 - 0} \right)}^2}} \) = \(\sqrt {10} \).

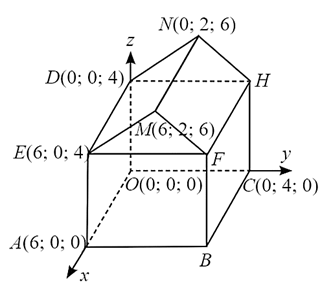
a) Ta có OABC là hình chữ nhật nên \(\overrightarrow {OA} = \overrightarrow {CB} = \left( {6;0;0} \right)\) ⇒ B(6; 4; 0).

              AEFB là hình chứ nhật nên \(\overrightarrow {AE} = \overrightarrow {BF} = \left( {0;0;4} \right)\) ⇒ F(6; 4; 4).

              DEFH là hình chữ nhật nên \(\overrightarrow {ED} = \overrightarrow {FH} = \left( {6;0;0} \right)\) ⇒ H(12; 4; 4).

b) Ta có: \(\overrightarrow {ME} \) = (0; −2; −2); \(\overrightarrow {MF} \) = (0; 2; −2).

c) Ta có: cos\(\widehat {EMF}\) = \(\frac{{\overrightarrow {ME} .\overrightarrow {MF} }}{{\left| {\overrightarrow {ME} } \right|.\left| {\overrightarrow {MF} } \right|}} = \frac{{0.0 + \left( { - 2} \right).2 + \left( { - 2} \right).\left( { - 2} \right)}}{{\sqrt {{0^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = 0\).

⇒ \(\widehat {EMF}\) = 90°.