Phương trình tiếp tuyến của đồ thị hàm số \({\rm{y}} = \frac{{\rm{x}}}{{{\rm{x}} - 1}}\) tại điểm có hoành độ bằng 2 là \({\rm{y}} = {\rm{ax}} + {\rm{b}}\) với \({\rm{a}},{\rm{b}} \in \mathbb{R}.\) Giá trị của biểu thức \({\rm{S}} = 4{\rm{a}} - 5\;{\rm{b}}\) là bao nhiêu?
Quảng cáo
Trả lời:
Đáp số: -24. \({{\rm{y}}^\prime } = \frac{{ - 1}}{{{{({\rm{x}} - 1)}^2}}},{\rm{y}}(2) = 2,{{\rm{y}}^\prime }(2) = - 1,{\rm{y}} = {{\rm{y}}^\prime }(2)({\rm{x}} - 2) + {\rm{y}}(2)\)
\( \Rightarrow {\rm{y}} = - 1({\rm{x}} - 2) + 2\) hay \({\rm{y}} = - {\rm{x}} + 4,{\rm{a}} = - 1,\;{\rm{b}} = 4,4{\rm{a}} - 5\;{\rm{b}} = - 24.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: 939.
Xét \(f(x) = 200\ln \left( {1 + \frac{{\rm{x}}}{{100}}} \right) + 1000 - {(x - 100)^2} - 200\) với \(x\) là số dương.
\({{\rm{f}}^\prime }({\rm{x}}) = \frac{{200}}{{{\rm{x}} + 100}} - 2({\rm{x}} - 100) = 0 \Leftrightarrow {\rm{x}} = 10\sqrt {101} \approx 100,5.\)
Lập bảng biến thiên từ đó suy ra lợi nhuận tối đa mỗi ngày nhà sản xuất thu được là \({\rm{f}}(100) \approx 938,63.\)
Lời giải
Đáp số: 20.
Xét \(C(x) = 4\ln x + {\left( {\frac{{30 - x}}{{10}}} \right)^2}\) với \(x \ge 10.\)
Ta có \({{\rm{C}}^\prime }({\rm{x}}) = \frac{4}{{\rm{x}}} - \frac{{30 - {\rm{x}}}}{{50}} = \frac{{{{\rm{x}}^2} - 30{\rm{x}} + 200}}{{50{\rm{x}}}} = \frac{{({\rm{x}} - 10)({\rm{x}} - 20)}}{{50{\rm{x}}}}.\)
Lập bảng biến thiên ta thấy \({\rm{C}}({\rm{x}})\) đạt giá trị nhỏ nhất khi \({\rm{x}} = 20.\)
Vậy nhà máy sản xuất 20 ấm mỗi ngày thì giá thành mỗi ấm là nhỏ nhất.
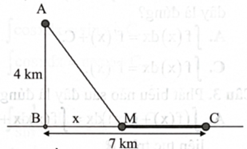
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.