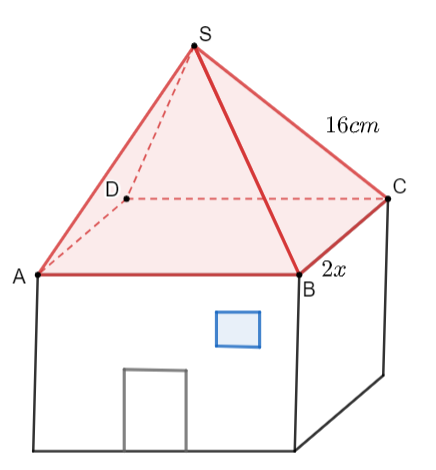
Bạn Nam làm một căn nhà đồ chơi bằng gỗ có phần mái là một chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn Nam dùng các thanh gỗ có chiều dài 16 cm. Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là 2x (cm). Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?
A. 512 cm2.
B. 256 cm2.
C. 128 cm2.
D. 1048 cm2.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Diện tích giấy màu cần sử dụng chỉnh bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng 16 cm và cạnh đáy bằng 2x cm.
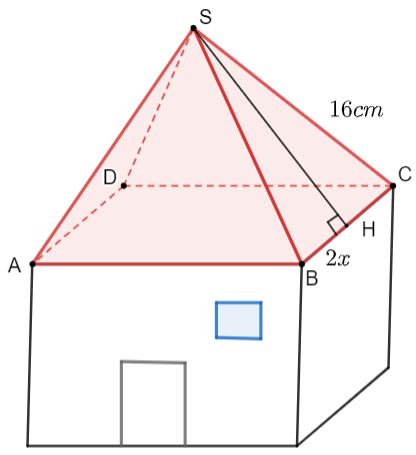
Xét tam giác SBC, kẻ đường cao SH vuông với BC tại H.
Do tam giác SBC cân tại S nên SH vừa là đường cao, vừa là đường trung trực.
Suy ra H là trung điểm của BC.
Suy ra BH = HC = \[\frac{{BC}}{2}\] = x cm (0 < x < 16).
Áp dụng định li Pythagore vào tam giác SHC, ta có:
SH2 + HC2 = SC2
SH2 = 162 – x2
SH2 = 256 – x2
SH = \(\sqrt {256 - {x^2}} \)
Diện tích tam giác SBC là \(\frac{1}{2}.2x.\sqrt {256 - {x^2}} = x\sqrt {256 - {x^2}} {\rm{ }}\)(cm2).
Diện tích giấy màu cần sử dụng là 4\(x\sqrt {256 - {x^2}} \)(cm2).
Thực hiện tính giá trị lớn nhất của S = 4\(x\sqrt {256 - {x^2}} \) với 0 < x < 16.
Ta có: \(4x\sqrt {256 - {x^2}} = 4\sqrt {256{x^2} - {x^4}} \)
\( = 4\sqrt { - \left( {{x^4} - 2.128{x^2} + {{128}^2}} \right) + {{128}^2}} \)
\( = 4\sqrt { - {{\left( {{x^2} - 128} \right)}^2} + {{128}^2}} \le 4\sqrt {{{128}^2}} = 512\).
Do đó, S ≤ 512.
Dấu “=” xảy ra khi x2 – 128 = 0 hay x = \(8\sqrt 2 \) (0 < x < 16).
Vậy diện tích giấy màu cần sử dụng nhiều nhất là 512 cm2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 21 triệu đồng.
B. 17 triệu đồng.
C. 19 triệu đồng.
D. 20 triệu đồng.
Lời giải
Đáp án đúng là: A
Gọi x là giá mà cửa hàng phải bán để sau khi giảm giá thu được lợi nhuận cao nhất (x > 0, triệu đồng).
Theo đề, số tiền mà của hàng sẽ giảm là 22 – x (triệu đồng) mỗi chiếc.
Khi đó, số lượng máy tính tăng lên là: 50(22 – x) : 0,2 = 250(22 – x) chiếc.
Do đó, số lượng máy tính mà doanh nghiệp bán được là:
500 + 250(22 – x) = 6000 – 250x (chiếc)
Doanh thu mà cửa hàng sẽ đạt được là: (6000 – 250x)x (triệu đồng).
Tiền mà cửa hàng bỏ ra để nhập máy tính sẽ là:
18(6000 – 250x) = 108000 – 4500x (triệu đồng)
Lợi nhuận mà cửa hàng thu được sau khi bán giá mới là:
(6000 – 250x)x – 108000 + 4500x = −250x2 + 10500x – 108000 (triệu đồng).
Ta có: −250x2 + 10500x – 108000 = −250(x – 21)2 + 2250 ≤ 2250.
Dấu “=” xảy ra khi −250(x – 21)2 = 0 suy ra x – 21 = 0 khi x = 21.
Vậy cửa hàng bán với giá 21 triệu đồng thì doanh thu nhận được là lớn nhất.
Câu 2
A. 169 m2.
B. 196 m2.
C. 144 m2.
D. 225 m2.
Lời giải
Đáp án đúng là: B
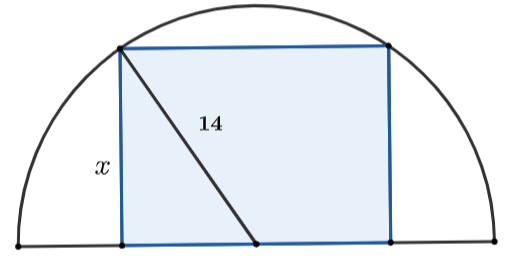
Gọi x là độ dài c
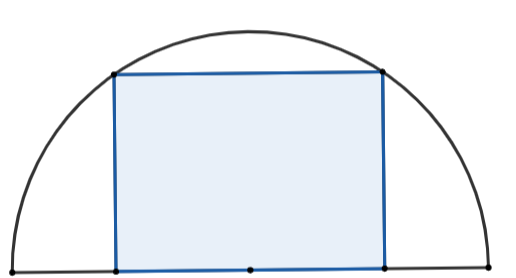
ạnh hình chữ nhật không nằm dọc theo đường kính đường tròn (0 < x < 14).Khi đó, độ dài cạnh của hình chữ nhật không nằm dọc trên đường tròn là: \[2\sqrt {{{14}^2} - {x^2}} {\rm{ }}\](m).
Diện tích hình chữ nhật là S = 2x\[\sqrt {{{14}^2} - {x^2}} {\rm{ }}\](m2).
Ta có: S2 = 4x2(196 – x2) = −4x4 + 4x2.196 – 1962 + 1962 = −(2x2 – 196)2 + 1962
Nhận thấy –(2x2 – 196)2 ≤ 0, do đó –(2x2 – 196)2 + 1962 ≤ 1962.
Suy ra S2 ≤ 1962, do đó S ≤ \[\sqrt {{{196}^2}} \] hay S ≤ 196 m2.
Dấu “=” xảy ra khi –(2x2 – 196)2 = 0 hay x = \[7\sqrt 2 \] (m).
Vậy diện tích lớn nhất của khu vui chơi đó là 196 m2.
Câu 3
A. x = 800.
B. x = 100.
C. x = 10.
D. x = 8.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Căng thành hình vuông với độ dài cạnh là 75 m.
B. Căng thành hình vuông với độ dài cạnh là 50 m.
C. Căng thành hình vuông với độ dài cạnh là 100 m.
D. Căng thành hình vuông với độ dài cạnh là 25 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.