12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
57 người thi tuần này 4.6 3 K lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. x = 800.
B. x = 100.
C. x = 10.
D. x = 8.
Lời giải
Đáp án đúng là: C
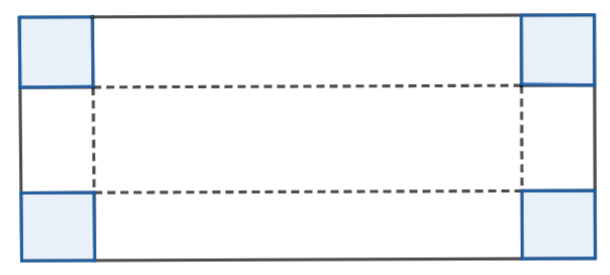
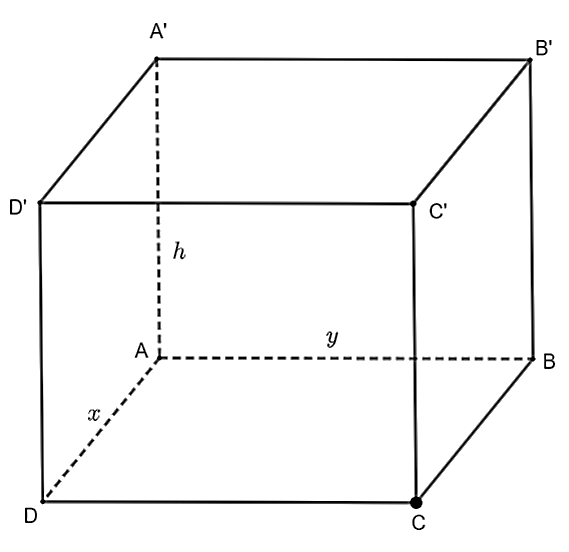
Diện tích tấm bìa hình chữ nhật này là: 50.30 = 1500 (cm2).
Chiều dài sau khi cắt tấm bìa là: 50 – 2x (cm).
Chiều rộng sau khi cắt tấm bìa là: 30 – 2x (cm).
Diện tích xung quanh của hộp là:
2x (50 – 2x + 30 – 2x) = 2x(80 – 4x) = −8x2 + 160x (cm2).
Diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất thì
−8x2 + 160x đạt giá trị lớn nhất.
Ta có: −8x2 + 160x = −8(x2 – 20x + 100) + 800 = −8(x – 10)2 + 800.
Nhận thấy −8(x – 10)2 ≤ 0 nên −8(x – 10)2 + 800 ≤ 800.
Dấu “=” xảy ra khi x – 10 = 0 hay x = 10.
Vậy diện tích xung quanh hình hộp chữ nhật là 800 cm2 khi x = 10 cm.
Câu 2
A. 21 triệu đồng.
B. 17 triệu đồng.
C. 19 triệu đồng.
D. 20 triệu đồng.
Lời giải
Đáp án đúng là: A
Gọi x là giá mà cửa hàng phải bán để sau khi giảm giá thu được lợi nhuận cao nhất (x > 0, triệu đồng).
Theo đề, số tiền mà của hàng sẽ giảm là 22 – x (triệu đồng) mỗi chiếc.
Khi đó, số lượng máy tính tăng lên là: 50(22 – x) : 0,2 = 250(22 – x) chiếc.
Do đó, số lượng máy tính mà doanh nghiệp bán được là:
500 + 250(22 – x) = 6000 – 250x (chiếc)
Doanh thu mà cửa hàng sẽ đạt được là: (6000 – 250x)x (triệu đồng).
Tiền mà cửa hàng bỏ ra để nhập máy tính sẽ là:
18(6000 – 250x) = 108000 – 4500x (triệu đồng)
Lợi nhuận mà cửa hàng thu được sau khi bán giá mới là:
(6000 – 250x)x – 108000 + 4500x = −250x2 + 10500x – 108000 (triệu đồng).
Ta có: −250x2 + 10500x – 108000 = −250(x – 21)2 + 2250 ≤ 2250.
Dấu “=” xảy ra khi −250(x – 21)2 = 0 suy ra x – 21 = 0 khi x = 21.
Vậy cửa hàng bán với giá 21 triệu đồng thì doanh thu nhận được là lớn nhất.
Câu 3
A. AB = BC = 4 m.
B. AB = 2 m, BC = 6 m.
C. AB = 3 m, BC = 5 m.
D. AB = 5 m, BC = 4 m.
Lời giải
Đáp án đúng là: A
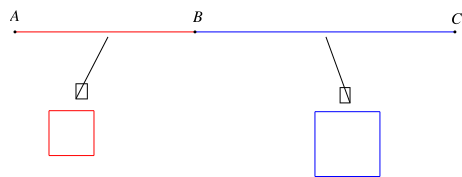
Gọi cạnh hình vuông được uốn từ đoạn AB là x (0 < x < 8, m).
Lúc này, độ dài đoạn AB chính là chu vi hình vuông đó và bằng 4x (m).
Do đó, độ dài đoạn BC là 8 – 4x (m).
Suy ra độ dài cạnh hình vuông được uốn bởi đoạn BC là \[\frac{{8 - 4x}}{4}\] = 2 – x (m).
Tổng diện tích hai hình vuông lúc này là x2 + (2 – x)2 (m2).
Ta có: x2 + (2 – x)2 = 2x2 – 4x + 4 = 2(x2 – 2x + 1) + 2 = 2(x – 1)2 + 2 ≥ 2.
Tổng diện tích hai hình vuông đạt giá trị nhỏ nhất bằng 2 m2 khi x – 1 = 0 hay
x = 1.
Khi đó, độ dài đoạn thẳng AB = 4 m và độ dài đoạn thẳng BC = 8 – 4 = 4 m hay B là trung điểm của đoạn AC.
Vậy để tổng diện tích hai hình vuông đạt giá trị lớn nhất thì ta chia đoạn dây thép thành hai phần bằng nhau AB = BC = 4 m.
Câu 4
A. Căng thành hình vuông với độ dài cạnh là 75 m.
B. Căng thành hình vuông với độ dài cạnh là 50 m.
C. Căng thành hình vuông với độ dài cạnh là 100 m.
D. Căng thành hình vuông với độ dài cạnh là 25 m.
Lời giải
Đáp án đúng là: A
• Gọi kích thước hình chữ nhật mà tể tướng sẽ căng là x và y (0 < x, y < 150).
Khi đó, ta có chu vi mảnh đất hình chữ nhật đó là 300 m,
suy ra x + y = 300 : 2 = 150 (m).
Diện tích của mảnh đất là S = xy (m2).
• Chứng minh bổ đề: \[\frac{{{{\left( {x + y} \right)}^2}}}{4} \ge xy\] với mọi x, y > 0.
Thật vậy, với mọi x, y > 0, ta có:
(x – y)2 ≥ 0
x2 – 2xy + y2 ≥ 0
(x + y)2 – 4xy ≥ 0
\[\frac{{{{\left( {x + y} \right)}^2}}}{4} \ge xy\].
Đẳng thức xảy ra khi x = y.
Áp dụng bất đẳng thức trên, ta có: \[S = xy \le \frac{{{{\left( {x + y} \right)}^2}}}{4}\]
Suy ra S ≤ \[\frac{{{{150}^2}}}{4}\] = 5 625.
Dấu “=” xảy ra khi x = y = \[\frac{{150}}{4}\] = 75 m.
Vậy tể tướng đó cần căng sợi dây bao quanh mảnh đất hình vuông có cạnh 75 m để mảnh đất nhận được có diện tích lớn nhất.
Câu 5
A. 512 cm2.
B. 256 cm2.
C. 128 cm2.
D. 1048 cm2.
Lời giải
Đáp án đúng là: A
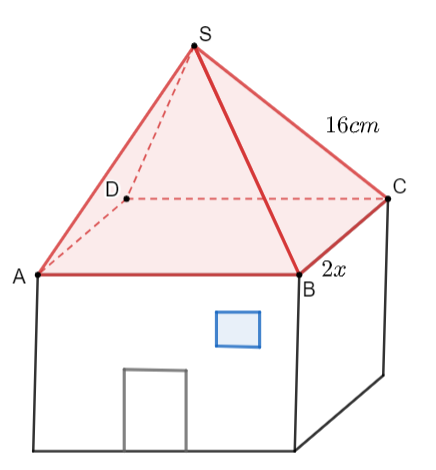
Diện tích giấy màu cần sử dụng chỉnh bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng 16 cm và cạnh đáy bằng 2x cm.
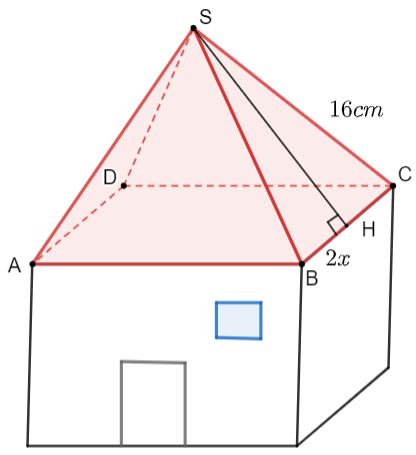
Xét tam giác SBC, kẻ đường cao SH vuông với BC tại H.
Do tam giác SBC cân tại S nên SH vừa là đường cao, vừa là đường trung trực.
Suy ra H là trung điểm của BC.
Suy ra BH = HC = \[\frac{{BC}}{2}\] = x cm (0 < x < 16).
Áp dụng định li Pythagore vào tam giác SHC, ta có:
SH2 + HC2 = SC2
SH2 = 162 – x2
SH2 = 256 – x2
SH = \(\sqrt {256 - {x^2}} \)
Diện tích tam giác SBC là \(\frac{1}{2}.2x.\sqrt {256 - {x^2}} = x\sqrt {256 - {x^2}} {\rm{ }}\)(cm2).
Diện tích giấy màu cần sử dụng là 4\(x\sqrt {256 - {x^2}} \)(cm2).
Thực hiện tính giá trị lớn nhất của S = 4\(x\sqrt {256 - {x^2}} \) với 0 < x < 16.
Ta có: \(4x\sqrt {256 - {x^2}} = 4\sqrt {256{x^2} - {x^4}} \)
\( = 4\sqrt { - \left( {{x^4} - 2.128{x^2} + {{128}^2}} \right) + {{128}^2}} \)
\( = 4\sqrt { - {{\left( {{x^2} - 128} \right)}^2} + {{128}^2}} \le 4\sqrt {{{128}^2}} = 512\).
Do đó, S ≤ 512.
Dấu “=” xảy ra khi x2 – 128 = 0 hay x = \(8\sqrt 2 \) (0 < x < 16).
Vậy diện tích giấy màu cần sử dụng nhiều nhất là 512 cm2.
Câu 6
A. x = 3,78 m.
B. x = 3,8 m.
C. x = 4,7 m.
D. x = 3,77 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{27}}{2}\) dm.
B. \(\frac{4}{3}\) dm.
C. \(\frac{3}{4}\) dm.
D. \(\frac{1}{2}\) dm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. AH = \[\frac{{3\sqrt 2 }}{2}\] cm.
B. AH = \[\frac{{3\sqrt 2 }}{4}\] cm.
C. AH = \[\frac{{\sqrt 2 }}{2}\] cm.
D. AH = \[\frac{3}{2}\] cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 169 m2.
B. 196 m2.
C. 144 m2.
D. 225 m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.