Tập nghiệm của bất phương trình \({5^{x - 1}} \ge {5^{{x^2} - x - 9}}\) là
Tập nghiệm của bất phương trình \({5^{x - 1}} \ge {5^{{x^2} - x - 9}}\) là
A. \(\left[ { - 2;4} \right]\).
B. \(\left[ { - 4;2} \right]\).
Câu hỏi trong đề: 43 bài tập Phương trình và bất phương trình có lời giải !!
Quảng cáo
Trả lời:
Ta có: .
Vậy tập nghiệm của bất phương trình là . Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
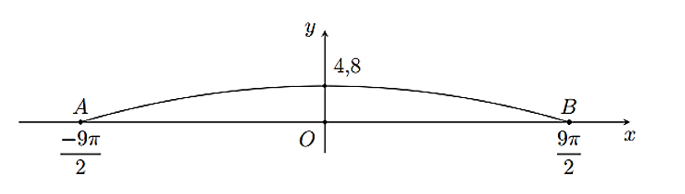
Ta có .
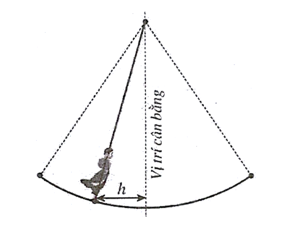
Vật ở xa vị trí cân bằng nhất nghĩa là .
Khi đó, . Vậy trong 10 giây đầu tiên thì vật ở xa vị trí cân bằng nhất tại các thời điểm (giây).
Khi vật ở vị trí cân bằng thì
.
Vậy trong khoảng từ 0 đến 20 giây thì vật ở vị trí cân bằng tại các thời điểm (giây); tức là có 5 lần vật qua vị trí cân bằng.
Đáp án: a) Đúng, b) Sai, c) Đúng, d) Sai.
Lời giải
Ta có .
Đáp án: a) Sai, b) Sai, c) Đúng, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.