Câu hỏi:

25/01/2025 79

Phương trình \[{\rm{sinx = }}\frac{{\rm{x}}}{{{\rm{2019}}}}\] có bao nhiêu nghiệm thực?

A. 1290.

B. 1287.

C. 1289.

D. 1288.

Xem lời giải

Câu hỏi trong đề: 10 câu trắc nghiệm Toán 11 Cánh diều Hàm số lượng giác và đồ thị có đáp án !!

Bắt đầu thi

Trả lời:

Giải bởi Vietjack

Đk:\[ - 2019 \le {\rm{x}} \le 2019\]

Nhận xét x = 0 là nghiệm của phương trình.

Nếu \[{\rm{x = }}{{\rm{x}}_{\rm{0}}}\] là nghiệm của phương trình thì \[x {\rm{ = }} - {{\rm{x}}_0}\] cũng là nghiệm của phương trình

Ta xét nghiệm của phương trình trên đoạn \[\left[ {{\rm{0; 2019}}} \right]\]. Vẽ đồ thị của hàm số \[{\rm{y = sinx}}\] và \[{\rm{y = }}\frac{{\rm{x}}}{{{\rm{2019}}}}\]. Ta thấy

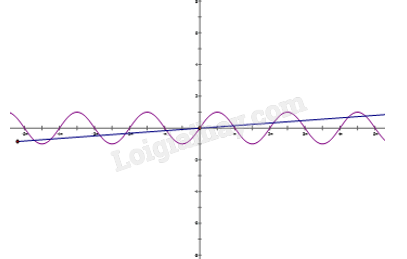
Phương trình s i n x = x 2019 có bao nhiêu nghiệm thực? (ảnh 1)

Trên đoạn \[\left[ {{\rm{0; 2\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{2\pi ; 4\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{4\pi ; 6\pi }}} \right]\] phương trình có hai nghiệm phân biệt

…

Trên nửa khoảng \[\left( {{\rm{640\pi ; 642\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{642\pi ; 2019}}} \right]\]phương trình có hai nghiệm phân biệt.

Như vậy trên đoạn \[\left[ {{\rm{0; 2019}}} \right]\]phương trình có một nghiệm x = 0 và \[{\rm{321x2 + 1 = 643}}\]nghiệm dương phân biệt. Mà do \[{\rm{x = }}{{\rm{x}}_0}\] là nghiệm của phương trình thì \[{\rm{x = }} - {{\rm{x}}_0}\] cũng là nghiệm của phương trình nên trên nửa khoảng \[\left[ { - {\rm{2019; }}0} \right)\]phương trình cũng có 643 nghiệm âm phân biệt.

Do đó trên đoạn \[\left[ { - 2019;2019} \right]\]phương trình có số nghiệm thực là \[{\rm{643x2 + 1 = 1287}}\]nghiệm

Vậy số nghiệm thực của phương trình đã cho là 1287 nghiệm.

Đáp án cần chọn là: B

Bình luận

Câu 1:

Cho hàm số f(x) có bảng biến thiên như sau

Số nghiệm thuộc đoạn\[\left[ { - \frac{{{\rm{3\pi }}}}{{\rm{2}}}{\rm{; 2\pi }}} \right]\]của phương trình\[{\rm{3f}}\left( {{\rm{cos2x}}} \right) - {\rm{4 = 0}}\]là

A. 14

B. 3

C. 11

D. 16

Xem đáp án » 25/01/2025 110

Câu 2:

Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số \[{\rm{y = 4sin}}\left| {\frac{{\rm{\pi }}}{{{\rm{178}}}}\left( {{\rm{t}} - {\rm{60}}} \right)} \right|{\rm{ + 10}}\], với \[t \in Z\]và \[{\rm{0 < t}} \le {\rm{365}}\]. Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất ?.

A.28 tháng 5.

B.29 tháng 5.

C.30 tháng 5.

D.31 tháng 5.

Xem đáp án » 25/01/2025 92

Câu 3:

Tìm chu kì của hàm số\[{\rm{f}}\left( {\rm{x}} \right){\rm{ = sin}}\frac{{\rm{x}}}{{\rm{2}}}{\rm{ + 2cos}}\frac{{{\rm{3x}}}}{{\rm{2}}}\]

A. \(5\pi \)

B. \(\frac{\pi }{2}\)

C. \(4\pi \)

D. \(2\pi \)

Xem đáp án » 25/01/2025 88

Câu 4:

Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h(m) của con kênh tính theo thời gian t (giờ) trong một ngày được cho bởi công thức:\[{\rm{h = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{cos}}\left( {\frac{{{\rm{\pi t}}}}{{\rm{8}}}{\rm{ + }}\frac{{\rm{\pi }}}{{\rm{4}}}} \right){\rm{ + 3}}\]. Thời điểm mực nước của kênh cao nhất là:

A. t = 15

B. t = 16

C. t = 13

D. t = 14

Xem đáp án » 25/01/2025 71

Câu 5:

Tìm m để bất phương trình\[\frac{{{\rm{3sin2x + cos2x}}}}{{{\rm{sin2x + 4co}}{{\rm{s}}^{\rm{2}}}{\rm{x + 1}}}} \le {\rm{m + 1}}\]đúng với mọi\[{\rm{x}} \in \mathbb{R}\]

A. \[{\rm{m}} \ge \frac{{3\sqrt 5 }}{4}\]

B. \[{\rm{m}} \ge \frac{{3\sqrt 5 + 9}}{4}\]

C. \[{\rm{m}} \ge \frac{{\sqrt {65} - 9}}{4}\]

D. \[{\rm{m}} \ge \frac{{3\sqrt 5 - 9}}{4}\]

Xem đáp án » 25/01/2025 64

Câu 6:

Cho hàm số \[{\rm{f}}\left( {\rm{x}} \right){\rm{ = 2}}{{\rm{x}}^{\rm{2}}} - {\rm{4x + 1}}\]. Tìm giá trị lớn nhất của hàm số \[{\rm{y = f}}\left( {{\rm{sinx}}} \right){\rm{; x}} \in \left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right]\]

A. 6

B. \[\frac{{13}}{2}\]

C. \[\frac{{11}}{2}\]

D. \[\frac{9}{2}\]

Xem đáp án » 25/01/2025 63

Phương trình \[{\rm{sinx = }}\frac{{\rm{x}}}{{{\rm{2019}}}}\] có bao nhiêu nghiệm thực?

Bình luận

Cho hàm số f(x) có bảng biến thiên như sau

Số nghiệm thuộc đoạn\[\left[ { - \frac{{{\rm{3\pi }}}}{{\rm{2}}}{\rm{; 2\pi }}} \right]\]của phương trình\[{\rm{3f}}\left( {{\rm{cos2x}}} \right) - {\rm{4 = 0}}\]là

Tìm chu kì của hàm số\[{\rm{f}}\left( {\rm{x}} \right){\rm{ = sin}}\frac{{\rm{x}}}{{\rm{2}}}{\rm{ + 2cos}}\frac{{{\rm{3x}}}}{{\rm{2}}}\]

Tìm m để bất phương trình\[\frac{{{\rm{3sin2x + cos2x}}}}{{{\rm{sin2x + 4co}}{{\rm{s}}^{\rm{2}}}{\rm{x + 1}}}} \le {\rm{m + 1}}\]đúng với mọi\[{\rm{x}} \in \mathbb{R}\]

Cho hàm số \[{\rm{f}}\left( {\rm{x}} \right){\rm{ = 2}}{{\rm{x}}^{\rm{2}}} - {\rm{4x + 1}}\]. Tìm giá trị lớn nhất của hàm số \[{\rm{y = f}}\left( {{\rm{sinx}}} \right){\rm{; x}} \in \left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right]\]

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

Phương trình \[{\rm{sinx = }}\frac{{\rm{x}}}{{{\rm{2019}}}}\] có bao nhiêu nghiệm thực?

Bình luận

Cho hàm số f(x) có bảng biến thiên như sau Số nghiệm thuộc đoạn\[\left[ { - \frac{{{\rm{3\pi }}}}{{\rm{2}}}{\rm{; 2\pi }}} \right]\]của phương trình\[{\rm{3f}}\left( {{\rm{cos2x}}} \right) - {\rm{4 = 0}}\]là

Tìm chu kì của hàm số\[{\rm{f}}\left( {\rm{x}} \right){\rm{ = sin}}\frac{{\rm{x}}}{{\rm{2}}}{\rm{ + 2cos}}\frac{{{\rm{3x}}}}{{\rm{2}}}\]

Tìm m để bất phương trình\[\frac{{{\rm{3sin2x + cos2x}}}}{{{\rm{sin2x + 4co}}{{\rm{s}}^{\rm{2}}}{\rm{x + 1}}}} \le {\rm{m + 1}}\]đúng với mọi\[{\rm{x}} \in \mathbb{R}\]

Cho hàm số \[{\rm{f}}\left( {\rm{x}} \right){\rm{ = 2}}{{\rm{x}}^{\rm{2}}} - {\rm{4x + 1}}\]. Tìm giá trị lớn nhất của hàm số \[{\rm{y = f}}\left( {{\rm{sinx}}} \right){\rm{; x}} \in \left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right]\]

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số f(x) có bảng biến thiên như sau

Số nghiệm thuộc đoạn\[\left[ { - \frac{{{\rm{3\pi }}}}{{\rm{2}}}{\rm{; 2\pi }}} \right]\]của phương trình\[{\rm{3f}}\left( {{\rm{cos2x}}} \right) - {\rm{4 = 0}}\]là