10 câu trắc nghiệm Toán 11 Cánh diều Hàm số lượng giác và đồ thị có đáp án

Chu kỳ của\[{\rm{sin}}\frac{{\rm{x}}}{{\rm{2}}}\]là \[{{\rm{T}}_{\rm{1}}}{\rm{ = }}\frac{{{\rm{2\pi }}}}{{\left| {\frac{{\rm{1}}}{{\rm{2}}}} \right|}}{\rm{ = 4\pi }}\]và Chu kỳ của\[{\rm{cos}}\frac{{{\rm{3x}}}}{{\rm{2}}}\]là \[{{\rm{T}}_{\rm{2}}}{\rm{ = }}\frac{{{\rm{2\pi }}}}{{\left| {\frac{{\rm{3}}}{{\rm{2}}}} \right|}}{\rm{ = }}\frac{{{\rm{4\pi }}}}{{\rm{3}}}\]

Chu kì của hàm ban đầu là bội chung nhỏ nhất của hai chu kì T₁ và T₂ vừa tìm được ở trên.

Chu kì của hàm ban đầu \[{\rm{T = 4\pi }}\]Đáp án cần chọn là: C

Xét hàm số\[{\rm{y = sinx}}\] trên đoạn\[\left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{;}} - \frac{{\rm{\pi }}}{{\rm{3}}}} \right]\] 

Hàm số đồng biến trên khoảng\[\left( { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{;}} - \frac{{\rm{\pi }}}{{\rm{3}}}} \right)\]

Vậy\[\mathop {{\rm{max}}}\limits_{\left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{;}} - \frac{{\rm{\pi }}}{{\rm{3}}}} \right]} {\rm{y = sin}}\left( { - \frac{{\rm{\pi }}}{{\rm{3}}}} \right){\rm{ = }} - \frac{{\sqrt {\rm{3}} }}{{\rm{2}}}\];\[\mathop {{\rm{min}}}\limits_{\left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{;}} - \frac{{\rm{\pi }}}{{\rm{3}}}} \right]} {\rm{y = sin}}\left( { - \frac{{\rm{\pi }}}{{\rm{2}}}} \right){\rm{ = }} - {\rm{1}}\]

Đáp án cần chọn là: B

\[{\rm{y = sinx; y = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{sin2x; y = }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{sin3x}}\] có chu kì tuần hoàn lần lượt là\[{\rm{2\pi ; \pi ; }}\frac{{{\rm{2\pi }}}}{{\rm{3}}}\] nên hàm số\[{\rm{y = sinx + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{sin2x + }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{sin3x}}\]có  chu kì tuần hoàn bội chung nhỏ nhất của\[{\rm{2\pi ; \pi ; }}\frac{{{\rm{2\pi }}}}{{\rm{3}}}\]

Vậy\[{\rm{y = sinx + }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{sin2x + }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{sin3x}}\] có  chu kì tuần hoàn là\(2\pi \)

Đáp án cần chọn là: A

\[{\rm{y = f}}\left( {\rm{x}} \right){\rm{ = }}\frac{{\rm{1}}}{{{\rm{si}}{{\rm{n}}^{\rm{3}}}{\rm{x}}}}\]có tập xác định D.\[{\rm{D = }}\left\{ {\left. {{\rm{x}} \in \mathbb{R}} \right|\sin {\rm{x}} \ne 0} \right\}\]

Ta có\[{\rm{sinx}} \ne 0 \Rightarrow {\rm{sin}}\left( { - {\rm{x}}} \right) \ne 0 \Rightarrow \forall {\rm{x}} \in {\rm{D}} \Rightarrow - {\rm{x}} \in {\rm{D}}\]

\[{\rm{f}}\left( { - {\rm{x}}} \right){\rm{ = }}\frac{{\rm{1}}}{{{\rm{si}}{{\rm{n}}^{\rm{3}}}\left( { - {\rm{x}}} \right)}}{\rm{ = }} - \frac{{\rm{1}}}{{{\rm{si}}{{\rm{n}}^{\rm{3}}}{\rm{x}}}} \Rightarrow {\rm{f}}\left( { - {\rm{x}}} \right){\rm{ = }} - {\rm{f}}\left( {\rm{x}} \right)\]

Từ đó suy ra hàm số\[{\rm{y = f}}\left( {\rm{x}} \right){\rm{ = }}\frac{{\rm{1}}}{{{\rm{si}}{{\rm{n}}^{\rm{3}}}{\rm{x}}}}\] là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.

Đáp án cần chọn là: A

Đk:\[ - 2019 \le {\rm{x}} \le 2019\]

Nhận xét x = 0 là nghiệm của phương trình.

Nếu \[{\rm{x = }}{{\rm{x}}_{\rm{0}}}\] là nghiệm của phương trình thì \[x {\rm{ = }} - {{\rm{x}}_0}\] cũng là nghiệm của phương trình

Ta xét nghiệm của phương trình trên đoạn \[\left[ {{\rm{0; 2019}}} \right]\]. Vẽ đồ thị của hàm số \[{\rm{y = sinx}}\] và \[{\rm{y = }}\frac{{\rm{x}}}{{{\rm{2019}}}}\]. Ta thấy

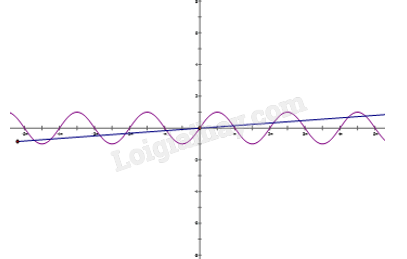
Trên đoạn \[\left[ {{\rm{0; 2\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{2\pi ; 4\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{4\pi ; 6\pi }}} \right]\] phương trình có hai nghiệm phân biệt

…

Trên nửa khoảng \[\left( {{\rm{640\pi ; 642\pi }}} \right]\]phương trình có hai nghiệm phân biệt

Trên nửa khoảng \[\left( {{\rm{642\pi ; 2019}}} \right]\]phương trình có hai nghiệm phân biệt.

Như vậy trên đoạn \[\left[ {{\rm{0; 2019}}} \right]\]phương trình có một nghiệm x = 0 và \[{\rm{321x2 + 1 = 643}}\]nghiệm dương phân biệt. Mà do \[{\rm{x = }}{{\rm{x}}_0}\] là nghiệm của phương trình thì \[{\rm{x = }} - {{\rm{x}}_0}\] cũng là nghiệm của phương trình nên trên nửa khoảng \[\left[ { - {\rm{2019; }}0} \right)\]phương trình cũng có 643 nghiệm âm phân biệt.

Do đó trên đoạn \[\left[ { - 2019;2019} \right]\]phương trình có số nghiệm thực là \[{\rm{643x2 + 1 = 1287}}\]nghiệm

Vậy số nghiệm thực của phương trình đã cho là 1287 nghiệm.

Đáp án cần chọn là: B

\[{\rm{x}} \in \left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right] \Rightarrow - 1 \le {\rm{sinx}} \le \frac{1}{2}\]

Đặt\[{\rm{t = sinx; x}} \in \left[ { - \frac{{\rm{\pi }}}{{\rm{2}}}{\rm{; }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right] \Rightarrow - 1 \le {\rm{t}} \le \frac{1}{2}\]

Ta có  có hoành độ đỉnh\[{\rm{t = }}1 \notin \left[ { - 1;\frac{1}{2}} \right]\]

Giá trị lớn nhất của hàm số là \[{\rm{f}}\left( { - 1} \right){\rm{ = 7}}\]

Giá trị lớn nhất của hàm số là \[{\rm{f}}\left( {\frac{{\rm{1}}}{{\rm{2}}}} \right){\rm{ = }}\frac{{\rm{7}}}{{\rm{2}}}\]

Đáp án cần chọn là: B