Câu 9-12 (4,0 điểm)
2) Cho \(\Delta ABC\) có \(AB < AC,\) nội tiếp đường tròn \(\left( O \right).\) Các đường cao \(AD,\,\,BE\) cắt nhau tại \(H.\)
1) Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn có đường kính \(AB = 1,2{\rm{\;m}}\) (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ hai).
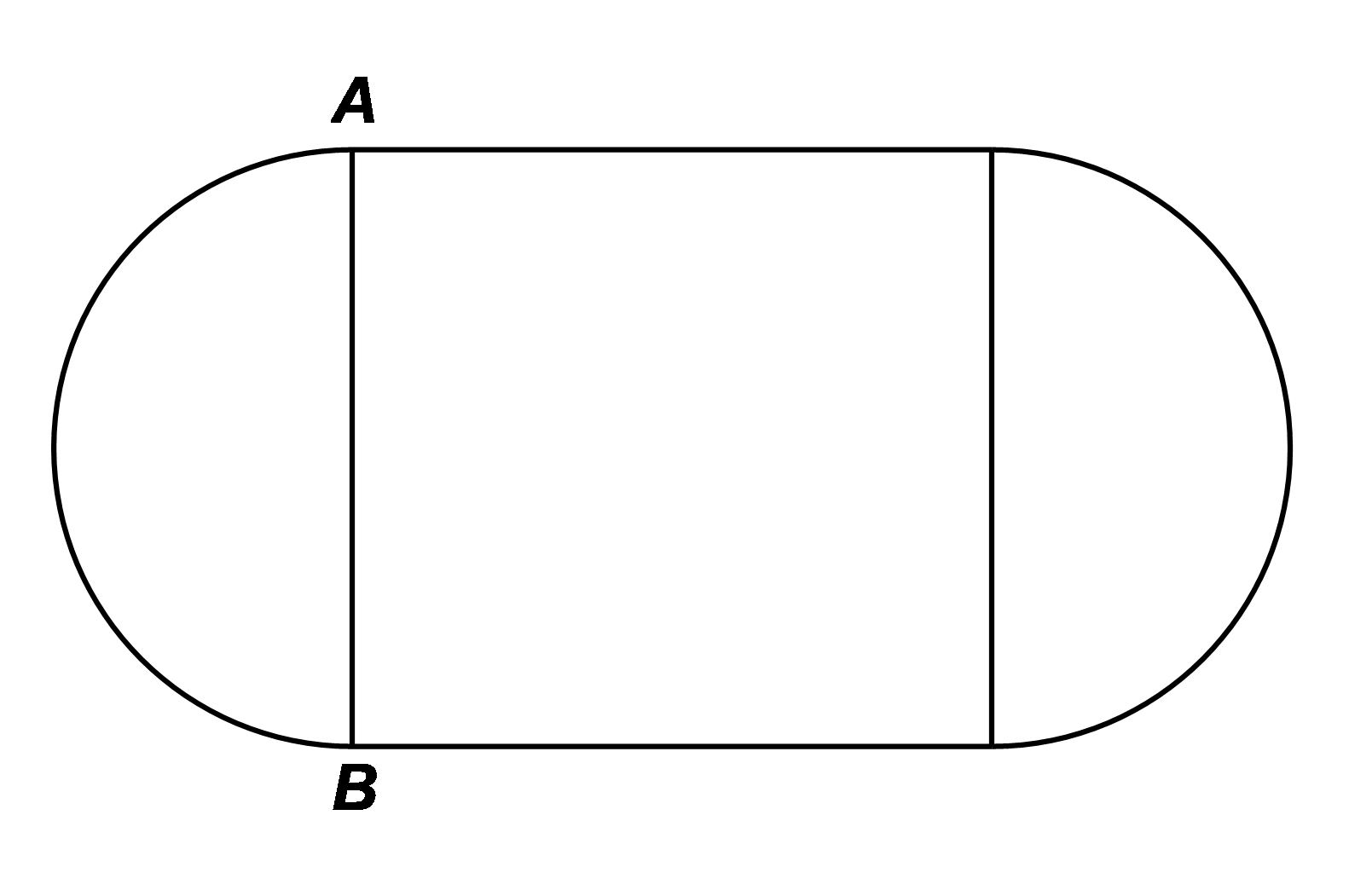 a) Tính diện tích mặt bàn.
b) Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một hình chữ nhật có một kích thước là \(AB\) (như hình vẽ). Hỏi kích thước còn lại của hình chữ nhật là bao nhiêu để diện tích mặt bàn tăng gấp ba lần sau khi nới?
a) Tính diện tích mặt bàn.
b) Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một hình chữ nhật có một kích thước là \(AB\) (như hình vẽ). Hỏi kích thước còn lại của hình chữ nhật là bao nhiêu để diện tích mặt bàn tăng gấp ba lần sau khi nới?
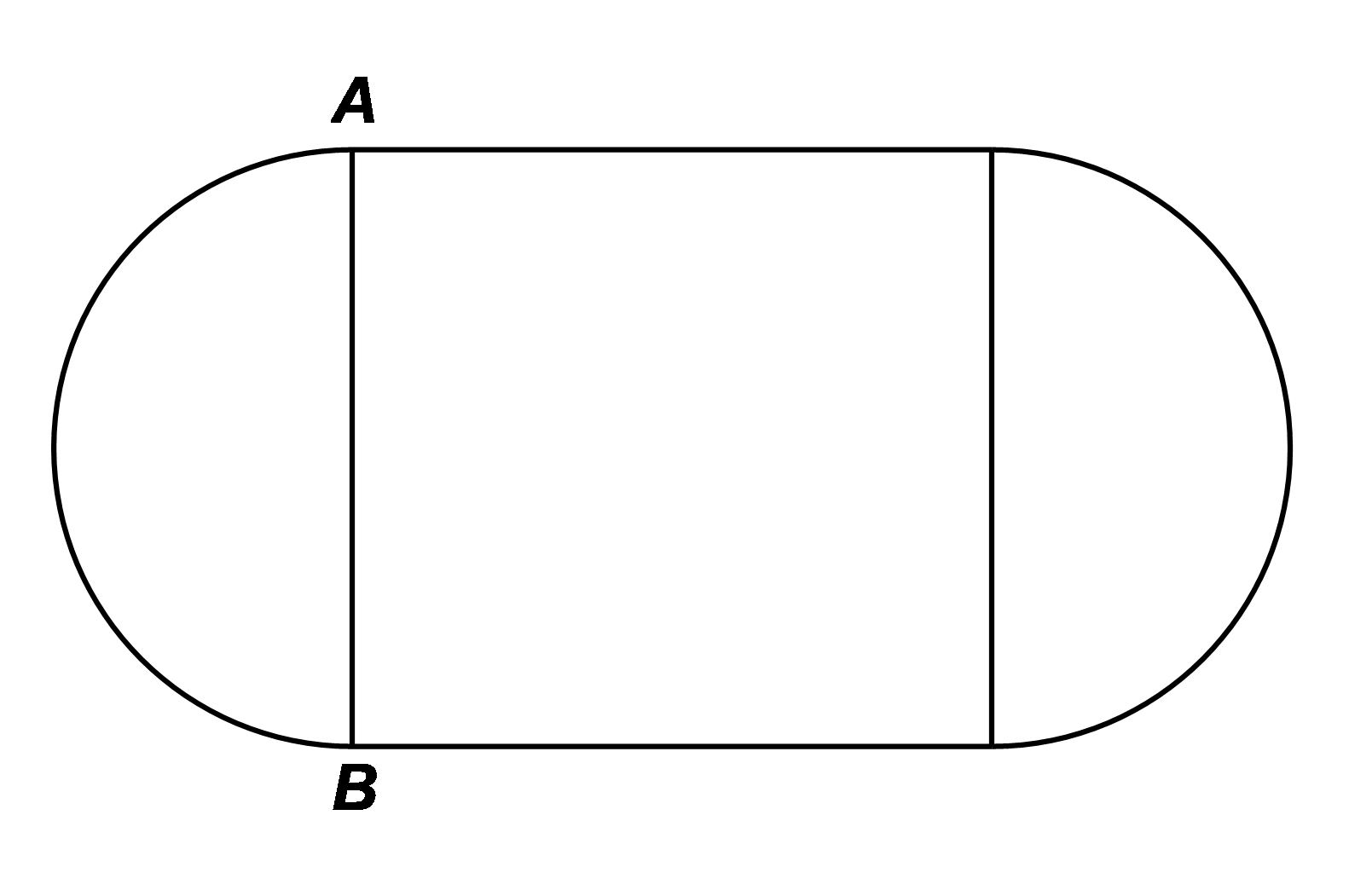
Quảng cáo
Trả lời:
a) Vì mặt bàn là hình tròn được ghép bởi hai nửa hình tròn có đường kính \(AB = 1,2{\rm{\;m}}\) nên bán kính của mặt bàn là: \(1,2:2 = 0,6{\rm{\;(m)}}{\rm{.}}\)
diện tích mặt bàn ban đầu là: \({S_1} = \pi \cdot 0,{6^2} = \frac{{9\pi }}{{25}} \approx 1,13{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
b) Vì diện tích mặt bàn tăng gấp ba lần sau khi nới, nên diện tích hình chữ nhật ghép thêm vào gấp 2 lần diện tích mặt bàn ban đầu là \({S_2} = 2{S_1} \approx 2 \cdot 1,13 = 2,26{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Kích thước còn lại của hình chữ nhật là: \(2,26:1,2 \approx 1,88{\rm{\;(m)}}{\rm{.}}\)
Câu hỏi cùng đoạn
Câu 2:
a) Chứng minh tứ giác \(ABDE\) nội tiếp.

Xét \(\Delta ABD\) vuông tại \(D\) nên đường tròn ngoại tiếp tam giác có tâm là trung điểm của cạnh huyền \(AB\) và bán kính bằng \(\frac{{AB}}{2}.\) Như vậy ba điểm \(A,\,\,B,\,\,D\) cùng nằm trên đường tròn đường kính \(AB.\)
Tương tự, \(\Delta ABE\) vuông tại \(E\) nên ba điểm \(A,\,\,B,\,\,E\) cùng nằm trên đường tròn đường kính \(AB.\)
Vậy bốn điểm \(A,\,\,B,\,\,D,\,\,E\) cùng nằm trên đường tròn đường kính \(AB\) hay tứ giác \(ABDE\) nội tiếp đường tròn đường kính \(AB.\)
Câu 3:
b) Kẻ vuông góc với tại Đường thẳng cắt theo thứ tự tại . Gọi là trung điểm của Chứng minh và
Do và nên suy ra (đồng vị).
Tứ giác nội tiếp nên (hai góc nội tiếp cùng chắn cung
Suy ra (1)
Chứng minh tương tự câu a), ta có tứ giác nội tiếp đường tròn đường kính nên (hai góc nội tiếp cùng chắn cung hay (2)
Từ (1) và (2) suy ra
⦁ Ta có nên (so le trong).
Tứ giác nội tiếp nên (hai góc nội tiếp cùng chắn cung hay Do đó
Xét và có: và
Do đó (g.g). Suy ra hay
Mà và (do lần lượt là trung điểm của
Suy ra hay
Câu 4:
c) Gọi \(I\) là giao điểm của tia \(MH\) với đường tròn \(\left( O \right).\) Chứng minh ba điểm \(I,\,A,\,N\) thẳng hàng.
Do (chứng minh ở câu b) nên \[\widehat {APQ} = \widehat {HCB}\] hay \[\widehat {APN} = \widehat {HCM}.\]
Từ câu b, có \(AP \cdot CM = PN \cdot HC\) suy ra \(\frac{{AP}}{{HC}} = \frac{{PN}}{{CM}}.\)
Xét \(\Delta APN\) và \(\Delta HCM\) có: \[\widehat {APN} = \widehat {HCM}\] và \(\frac{{AP}}{{HC}} = \frac{{PN}}{{CM}}.\)
Do đó (c.g.c). Suy ra \(\widehat {PAN} = \widehat {CHM}.\)
Mà \(\widehat {CHM} = \widehat {IHF}\) (đối đỉnh) nên \(\widehat {PAN} = \widehat {IHF}.\) (3)
Kẻ đường kính \(AK\) của đường tròn \(\left( O \right)\) và gọi \(F\) là giao điểm của \(CH\) và \(AB.\)
Xét \(\Delta ABC\) có hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\) nên \(H\) là trực tâm của tam giác, suy ra \(CF \bot AB\) tại \(F.\)
Xét đường tròn \(\left( O \right)\) có \(\widehat {ABK} = \widehat {ACK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(KB \bot AB,\,\,KC \bot AC.\)
Do đó \(BH\,{\rm{//}}\,KC\) (cùng vuông góc với \(AC)\) và \(CH\,{\rm{//}}\,KB\) (cùng vuông góc với \(AB)\)
Suy ra tứ giác \(BHCK\) là hình bình hành nên hai đường chéo \(BC,\,\,HK\) cắt nhau tại trung điểm của mỗi đường.
Xét \(\Delta OBC\) cân tại \(O\) (do \(OB = OC)\) nên đường cao \(OM\) đồng thời là đường trung tuyến của tam giác, hay \(M\) là trung điểm của \(BC.\)
Suy ra \(M\) là trung điểm của \(HK\) nên \(H,\,\,M,\,\,K\) thẳng hàng.
Do đó \(I,\,\,H,\,\,K\) thằng hàng nên \(\widehat {AIH} = \widehat {AIK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)).\)
\(\Delta AIH\) vuông tại \(I\) nên ba điểm \[A,\,\,I,\,\,H\] thuộc đường tròn đường kính \(AH.\)
\(\Delta AFH\) vuông tại \(F\) nên ba điểm \(A,\,\,F,\,\,H\) thuộc đường tròn đường kính \(AH.\)
Suy ra \(A,\,\,I,\,\,F,\,\,H\) cùng thuộc một đường tròn nên \(\widehat {IAF} = \widehat {IHF}\) (hai góc nội tiếp cùng chắn cung \(IF).\) (4)
Từ (3) và (4) suy ra \(\widehat {PAN} = \widehat {IAF}.\)
Lại có \(\widehat {PAN} + \widehat {NAF} = 180^\circ \) nên \(\widehat {NAF} + \widehat {IAF} = 180^\circ \) hay \(\widehat {NAI} = 180^\circ \)
Vậy ba điểm \(N,\,\,A,\,\,I\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Tần số ghép nhóm của nhóm là 6 .
Tần số tương đối ghép nhóm của nhóm là
Lời giải
Gọi \[x\] (m) là chiều rộng của đáy bể \[\left( {x > 0} \right).\]
Chiều dài của đáy bể là \[2x\] (m).
Chiều cao của bể là \[h\] (m).
Ta có \[V = 1 = 2x \cdot x \cdot h\] nên \[h = \frac{1}{{2{x^2}}}\] (m).
Diện tích xung quanh của bể là: \[{S_{xq}} = 2 \cdot \left( {2x + x} \right) \cdot \frac{1}{{2{x^2}}} = \frac{3}{x}\] (m2).
Diện tích đáy bể là: \({S_d} = x \cdot 2x = 2{x^2}\) (m2).
Chi phí tiền để làm bể cá là: \[T = \frac{{500}}{2} \cdot \frac{3}{x} + 500 \cdot 2{x^2} = \frac{{750}}{x} + 1\,\,000{x^2}\] (nghìn đồng).
Để chi phí làm bể cá là tối thiểu thì ta đi tìm giá trị nhỏ nhất của \(T.\)
Ta có \[T = \frac{{750}}{x} + 1\,\,000{x^2} = 1\,\,000{x^2} + \frac{{375}}{x} + \frac{{375}}{x}\]
\[ \ge 3\sqrt[3]{{1\,\,000{x^2} \cdot \frac{{375}}{x} \cdot \frac{{375}}{x}}}\] (BĐT Cauchy)
\[ = 750\sqrt[3]{9}.\]
Dấu “=” xảy ra khi và chỉ khi \[1\,\,000{x^2} = \frac{{375}}{x},\] hay \[x = \frac{{\sqrt[3]{3}}}{2}.\]
Vậy chi phí tối thiểu để làm bể cá là \[750\sqrt[3]{9} \approx 1\,\,560\] nghìn đồng \( = 1\,\,560\,\,000\) đồng, khi chiều rộng của đáy bể là \[\frac{{\sqrt[3]{3}}}{2}\] (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
