Cho \[\Delta ABC\] vuông tại \(A\) có 3 đỉnh thuộc \(\left( O \right),\) đường cao \(AH,\) biết\(AB = 6{\rm{\;cm,}}\,\,AC = 8{\rm{\;cm}}.\) Khi đó độ dài đường tròn có đường kính \(AH\) bằng
Quảng cáo
Trả lời:
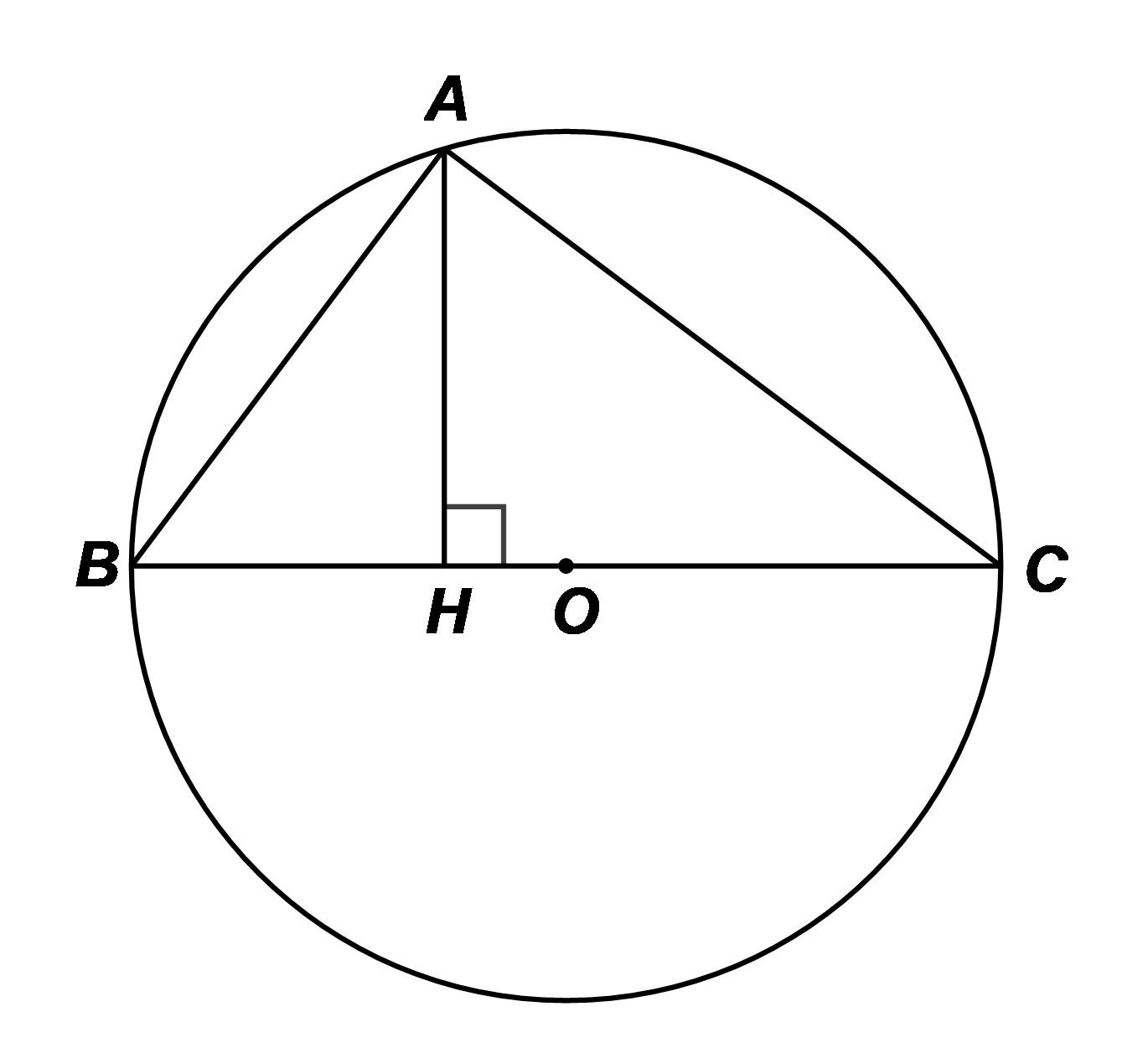
Đáp án đúng là: D
Do \[\Delta ABC\] vuông tại \(A\) nên đường tròn \(\left( O \right)\) là đường kính là \(BC.\)
Ta có: \[\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{A{C^2} + A{B^2}}}{{A{C^2} \cdot A{B^2}}} = \frac{{B{C^2}}}{{A{C^2} \cdot A{B^2}}} = \frac{{B{C^2}}}{{{{\left( {AC \cdot AB} \right)}^2}}}.\]Xét \(\Delta ABC\) và \(\Delta HBA\) có: \(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat {ABC}\) là góc chung
Do đó (g.g). Suy ra \(\frac{{AC}}{{HA}} = \frac{{BC}}{{BA}}\) hay \(AC \cdot AB = AH \cdot BC.\)
Khi đó, \[\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{B{C^2}}}{{{{\left( {AC \cdot AB} \right)}^2}}} = \frac{{B{C^2}}}{{{{\left( {AH \cdot BC} \right)}^2}}} = \frac{{B{C^2}}}{{A{H^2} \cdot B{C^2}}} = \frac{1}{{A{H^2}}}.\]
Nên \[\frac{1}{{A{H^2}}} = \frac{1}{{{6^2}}} + \frac{1}{{{8^2}}} = \frac{{25}}{{576}},\] suy ra \(A{H^2} = \frac{{576}}{{25}}\) do đó \(AH = \frac{{24}}{5} = 4,8{\rm{\;(cm)}}{\rm{.}}\)
Vậy độ dài đường tròn có đường kính \(AH\) bằng \(2\pi \cdot \frac{{4,8}}{2} = 4,8\pi {\rm{\;(cm)}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Với \(a > 0,\,\,a \ne 1,\) ta có:
\(A = \left( {\frac{{\sqrt a }}{{\sqrt a - 1}} + \frac{1}{{\sqrt a - a}}} \right):\left( {\frac{1}{{\sqrt a + 1}} + \frac{2}{{a - 1}}} \right)\)
\[ = \left[ {\frac{{\sqrt a }}{{\sqrt a - 1}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{1}{{\sqrt a + 1}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\]
\( = \left[ {\frac{{\sqrt a \cdot \sqrt a }}{{\sqrt a \left( {\sqrt a - 1} \right)}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{{\sqrt a - 1}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}}:\frac{{\sqrt a - 1 + 2}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}} \cdot \frac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}{{\sqrt a + 1}}\)
\( = \frac{{a - 1}}{{\sqrt a }}.\)
Vậy với \(a > 0,\,\,a \ne 1\) thì \(A = \frac{{a - 1}}{{\sqrt a }}.\)
Câu 2
A. \(24\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
B. \(12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
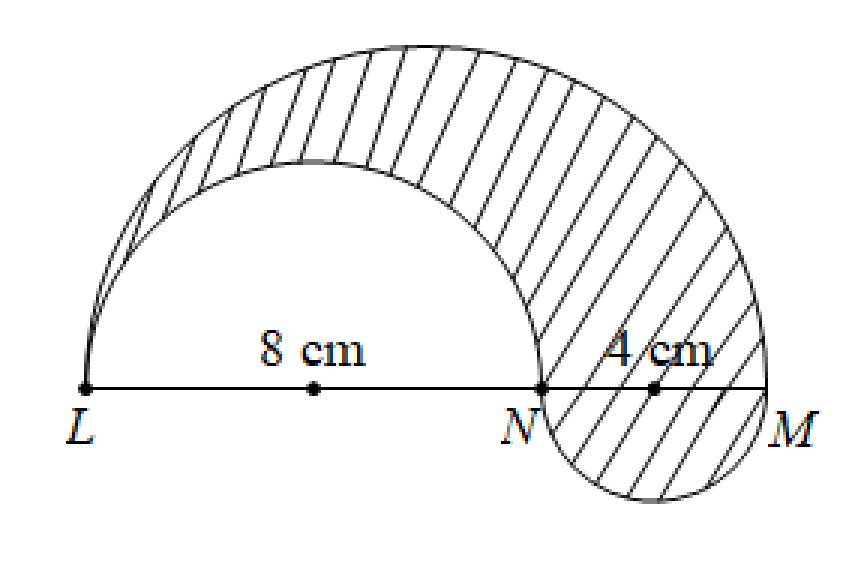
Ta có: \(LM = LN + NM = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LN\) là: \({S_1} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{8}{2}} \right)^2} = 8\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LM\) là: \({S_2} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{{12}}{2}} \right)^2} = 18\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(NM\) là: \({S_3} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{4}{2}} \right)^2} = 2\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích phần kẻ sọc ở hình đã cho là: \(S = {S_2} - {S_1} + {S_3} = 18\pi - 8\pi + 2\pi = 12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.