II. PHẦN TỰ LUẬN (7,0 điểm)

Câu 21-23. (2,5 điểm)

1) Rút gọn biểu thức \(A = \left( {\frac{{\sqrt a }}{{\sqrt a - 1}} + \frac{1}{{\sqrt a - a}}} \right):\left( {\frac{1}{{\sqrt a + 1}} + \frac{2}{{a - 1}}} \right)\) với \(a > 0,\,\,a \ne 1.\)

Hướng dẫn giải

Đáp án đúng là: B

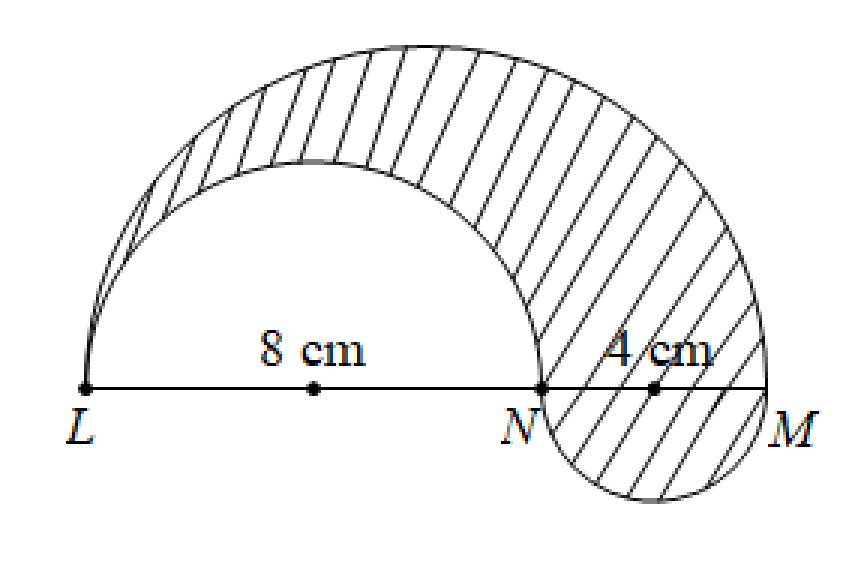
Ta có: \(LM = LN + NM = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)

Diện tích nửa hình tròn đường kính \(LN\) là: \({S_1} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{8}{2}} \right)^2} = 8\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích nửa hình tròn đường kính \(LM\) là: \({S_2} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{{12}}{2}} \right)^2} = 18\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích nửa hình tròn đường kính \(NM\) là: \({S_3} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{4}{2}} \right)^2} = 2\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Diện tích phần kẻ sọc ở hình đã cho là: \(S = {S_2} - {S_1} + {S_3} = 18\pi - 8\pi + 2\pi = 12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Hướng dẫn giải

Đáp án đúng là: D

Xét \(\Delta ABQ\) vuông tại \(B,\) ta có: \(AB = BQ \cdot \tan \widehat {BQA}\) suy ra \(BQ = \frac{{AB}}{{\tan \widehat {BQA}}} = \frac{{AB}}{{\tan 42^\circ }}{\rm{\;(m)}}{\rm{.}}\)

Xét \(\Delta ABP\) vuông tại \(B,\) ta có: \(AB = BP \cdot \tan \widehat {BPA}\) suy ra \(BP = \frac{{AB}}{{\tan \widehat {BPA}}} = \frac{{AB}}{{\tan 14^\circ }}{\rm{\;(m)}}{\rm{.}}\)

Ta có: \(PQ = BP - BQ\) nên \(300 = \frac{{AB}}{{\tan 14^\circ }} - \frac{{AB}}{{\tan 42^\circ }}\)

\(300 = AB\left( {\frac{1}{{\tan 14^\circ }} - \frac{1}{{\tan 42^\circ }}} \right)\)

\(AB = \frac{{300}}{{\frac{1}{{\tan 14^\circ }} - \frac{1}{{\tan 42^\circ }}}} \approx 103{\rm{\;(m)}}{\rm{.}}\)