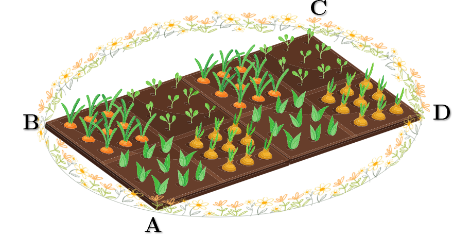
(0,5 điểm) Người ta muốn làm một vườn rau có dạng hình chữ nhật \(ABCD\) có diện tích \(640{\rm{\;}}{{\rm{m}}^2},\) để tạo thêm cảnh quan xung quanh đẹp hơn, người ta mở rộng thêm bốn phần diện tích để trồng hoa, tạo thành một đường tròn đi như hình vẽ, biết tâm hình tròn trùng với giao điểm hai đường chéo của hình chữ nhật. Khi đó chọn kích thước cạnh \(ABCD\) như thế nào để diện tích của bốn phần đất trồng hoa nhỏ nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi \(x,\,\,y{\rm{\;(m)}}\) lần lượt là chiều dài và chiều rộng của khu vườn hình chữ nhật \(ABCD\) \(\left( {x,\,\,y > 0} \right).\)
Vì độ dài đường kính của đường tròn là đường chéo của hình chữ nhật \(ABCD\) nên biểu thức xác định đường kính của đường tròn là \(\sqrt {{x^2} + {y^2}} {\rm{\;(m)}}\) (áp dụng định lí Pythagore).
Suy ra bán kính của đường tròn là \(\frac{{\sqrt {{x^2} + {y^2}} }}{2}{\rm{\;(m)}}{\rm{.}}\)
Diện tích đường tròn là \(S = \pi \cdot \frac{{{x^2} + {y^2}}}{4}{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích của hình chữ nhật là \({S_{hcn}} = xy = 640{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích phần đất trồng hoa là \(S' = S - {S_{hcn}} = \pi \cdot \frac{{{x^2} + {y^2}}}{4} - xy{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Với mọi \(x,\,\,y\) ta luôn có:
\({\left( {x - y} \right)^2} \ge 0\)
\({x^2} - 2xy + {y^2} \ge 0\)
\({x^2} + {y^2} \ge 2xy\)
\(\frac{{{x^2} + {y^2}}}{4} \ge \frac{{xy}}{2} > 0\)
\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} \ge \frac{{\pi xy}}{2}\)
\(\frac{{\pi \left( {{x^2} + {y^2}} \right)}}{4} - xy \ge \frac{{\pi xy}}{2} - xy\)
Do đó \(S' \ge \frac{{\pi xy}}{2} - xy = 320\pi - 640{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Dấu “=” xảy ra khi và chỉ khi \({\left( {x - y} \right)^2} = 0\) hay \(x = y.\)
Như vậy, để diện tích của bốn phần đất trồng hoa nhỏ nhất thì \(x = y.\)
Khi đó, ta có \(x = y\) và \(xy = 640\) nên \(x = y = \sqrt {640} = 8\sqrt {10} {\rm{\;(m)}}{\rm{.}}\)
Vậy mảnh vườn \(ABCD\) có hai kích thước bằng nhau và bằng \(8\sqrt {10} {\rm{\;m}}\) thì diện tích của bốn phần đất trồng hoa nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Với \(a > 0,\,\,a \ne 1,\) ta có:
\(A = \left( {\frac{{\sqrt a }}{{\sqrt a - 1}} + \frac{1}{{\sqrt a - a}}} \right):\left( {\frac{1}{{\sqrt a + 1}} + \frac{2}{{a - 1}}} \right)\)
\[ = \left[ {\frac{{\sqrt a }}{{\sqrt a - 1}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{1}{{\sqrt a + 1}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\]
\( = \left[ {\frac{{\sqrt a \cdot \sqrt a }}{{\sqrt a \left( {\sqrt a - 1} \right)}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{{\sqrt a - 1}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}}:\frac{{\sqrt a - 1 + 2}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}} \cdot \frac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}{{\sqrt a + 1}}\)
\( = \frac{{a - 1}}{{\sqrt a }}.\)
Vậy với \(a > 0,\,\,a \ne 1\) thì \(A = \frac{{a - 1}}{{\sqrt a }}.\)
Câu 2
A. \(24\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
B. \(12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
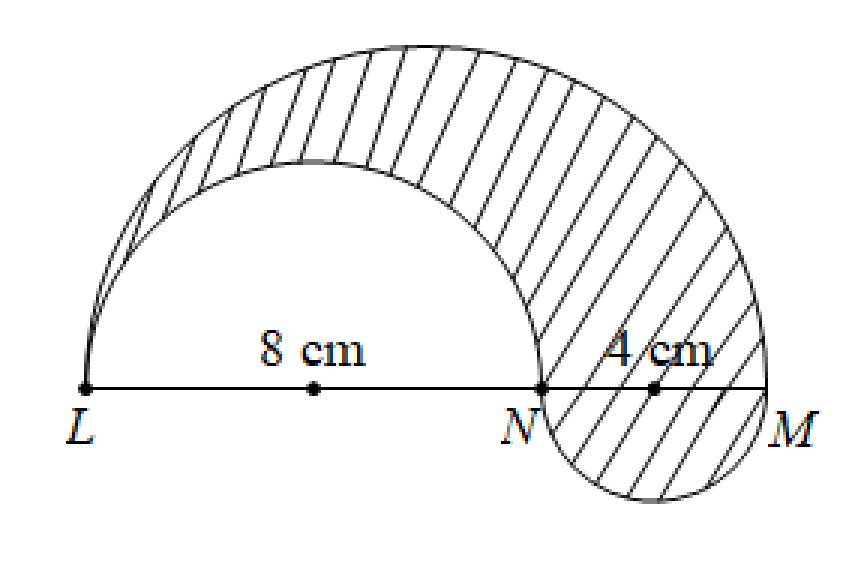
Ta có: \(LM = LN + NM = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LN\) là: \({S_1} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{8}{2}} \right)^2} = 8\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LM\) là: \({S_2} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{{12}}{2}} \right)^2} = 18\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(NM\) là: \({S_3} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{4}{2}} \right)^2} = 2\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích phần kẻ sọc ở hình đã cho là: \(S = {S_2} - {S_1} + {S_3} = 18\pi - 8\pi + 2\pi = 12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập