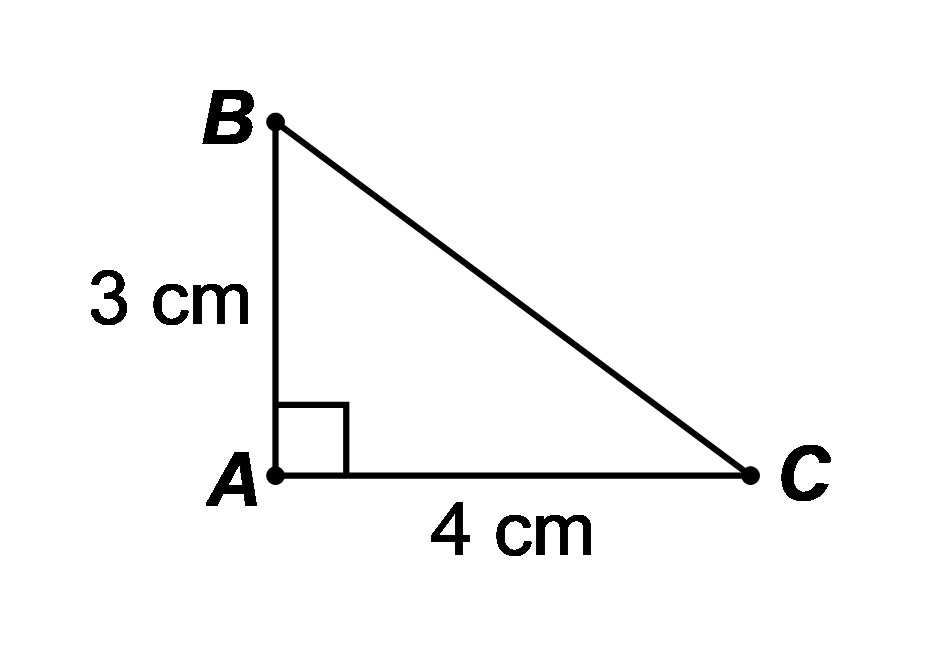
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3{\rm{\;(cm)}},\,\,AC = 4{\rm{\;(cm)}}{\rm{.}}\) Khẳng định nào sau đây là đúng?          

Đáp án đúng là: A

Đường tròn đi qua bốn đỉnh của hình chữ nhật \(MNPQ\) là đường tròn đường kính \(MP.\)

Xét \(\Delta MPQ\) vuông tại \(Q,\) theo định lí Pythagore, ta có:

\(M{P^2} = M{Q^2} + P{Q^2} = {5^2} + {12^2} = 169.\) Do đó \(MP = 13{\rm{\;cm}}.\)

Với \(x \ge 0,\,\,x \ne 1,\) ta có:

\(P = \frac{2}{{\sqrt x + 1}} + \frac{2}{{\sqrt x - 1}} + \frac{{\sqrt x - 5}}{{x - 1}}\)

\[ = \frac{{2\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{\sqrt x - 5}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]

\[ = \frac{{2\sqrt x - 2 + 2\sqrt x + 2 + \sqrt x - 5}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]

\[ = \frac{{5\sqrt x - 5}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\]

\[ = \frac{{5\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \frac{5}{{\sqrt x + 1}}.\]

Vậy với \(x \ge 0,\,\,x \ne 1\) thì \[P = \frac{5}{{\sqrt x + 1}}.\]