Một người đi xe đạp từ $A$ đến $B$ cách nhau 60 km. Sau 1 giờ 40 phút, trên cùng quãng đường đó, một xe máy đi từ $A$ đến $B$ và đến B sớm hơn xe đạp 1 giờ. Tính vận tốc của mỗi xe, biết rằng tốc độ của xe máy gấp 3 lần tốc độ của xe đạp.

Xem lời giải

Câu hỏi trong đề: 22 bài tập Phương trình quy về phương trình bậc nhất một ẩn có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

Gọi tốc độ của xe đạp là \[x\left( {km/h} \right),{\rm{ }}x > 0\].

Thời gian xe đạp đi quãng đường từ $A$ đến $B$ là $\frac{{60}}{x}$(giờ). Tốc độ của xe máy là $3x\left( {km/h} \right)$.

Thời gian xe máy đi quãng đường từ $A$ đến $B$ là $\frac{{60}}{{3x}} = \frac{{20}}{x}$(giờ).

Đổi 1 giờ 40 phút = $\frac{5}{3}$ giờ. Vì xe máy xuất phát sau xe đáp 1 giờ 40 phút và đến sớm hơn xe đạp 1 giờ nên ta có phương trình:

$\frac{{60}}{x} - \frac{{20}}{x} = \frac{5}{3} + 1$

$\frac{{40}}{x} = \frac{8}{3}$

$\frac{{40.3}}{{3x}} = \frac{{8x}}{{3x}}$

Vậy $x = 15$

Ta thấy $x = 15$ thoả mãn điều kiện $x > 0$. Vậy tốc độ của xe đạp là $15{\rm{ }}km/h$; tốc độ của xe máy là $45{\rm{ }}km/h$

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một khu đất có dạng hình chữ nhật với chiều dài hơn chiều rộng $16{\rm{\;m}}$. Trên khu đất đó, người ta làm một mảnh vườn trồng hoa có dạng hình thoi $ABCD$ với đường chéo $AC$ bằng chiều rộng của khu đất và đường chéo $BD$ bằng chiều dài của khu đất (Hình 1). Tính chiều dài của khu đất, Hinh 1 biết diện tích của phần đất còn lại là $96{\rm{\;}}{{\rm{m}}^2}$.

$Một khu đất có dạng hình chữ nhật với chiều dài hơn chiều rộng $16{\rm{\;m}}$. Trên khu đất đó, người ta làm một mảnh vườn trồng hoa có dạng hình thoi $ABCD$ với đường chéo $AC$ bằng ch (ảnh 1)$

Xem đáp án

Lời giải

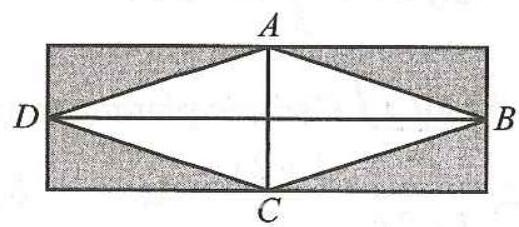
Gọi $x\left( {{\rm{\;m}}} \right)$ là chiều dài của khu đất với $x > 16$. Khi đó, chiều rộng của khu đất là $x - 16\left( {{\rm{\;m}}} \right)$ và mảnh vườn trồng hoa có $AC = x - 16\left( {{\rm{\;m}}} \right)$ và $BD = x\left( {{\rm{\;m}}} \right)$.

Do đó, diện tích của khu đất là: $\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)$ và diện tích của mảnh vườn trồng hoa là: $\frac{1}{2}\left( {x - 16} \right)x\left( {{\rm{\;}}{{\rm{m}}^2}} \right)$. Vì diện tích của phần đất còn lại là $96{\rm{\;}}{{\rm{m}}^2}$ nên ta có phương trình: $\left( {x - 16} \right)x - \frac{1}{2}\left( {x - 16} \right)x = 96$ hay $\frac{1}{2}\left( {x - 16} \right)x = 96$. Tức là, ${x^2} - 16x - 192 = 0$.

Giải phương trình:

${x^2} - 16x - 192 = 0$

$\left( {{x^2} - 16x + 64} \right) - 256 = 0$

${(x - 8)^2} - {16^2} = 0$

$\left( {x - 24} \right)\left( {x + 8} \right) = 0$

\[x = 24\] hoặc $x$$ = - 8$

Do $x > 16$ nên $x = 24$. Vậy chiều dài của khu đất là $24{\rm{\;m}}$.

Câu 2