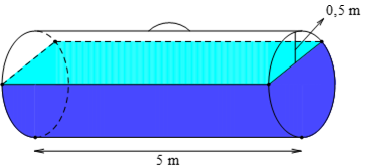
Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là $5m$, có bán kính đáy $1m$, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với $0,5m$ của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy $\pi \approx 3,14$, kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị ${m^3}$)

$Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy $\pi \approx 3,14$, kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị ${m^3}$) (ảnh 1)$ $Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (lấy $\pi \approx 3,14$, kết quả làm tròn đến chữ số thập phân thứ hai, theo đơn vị ${m^3}$) (ảnh 2)$

Xem lời giải

Câu hỏi trong đề: 123 bài tập Nón trụ cầu và hình khối có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có: $HO = OC - CH = 1 - \frac{1}{2} = \frac{1}{2}$ $\left( m \right)$
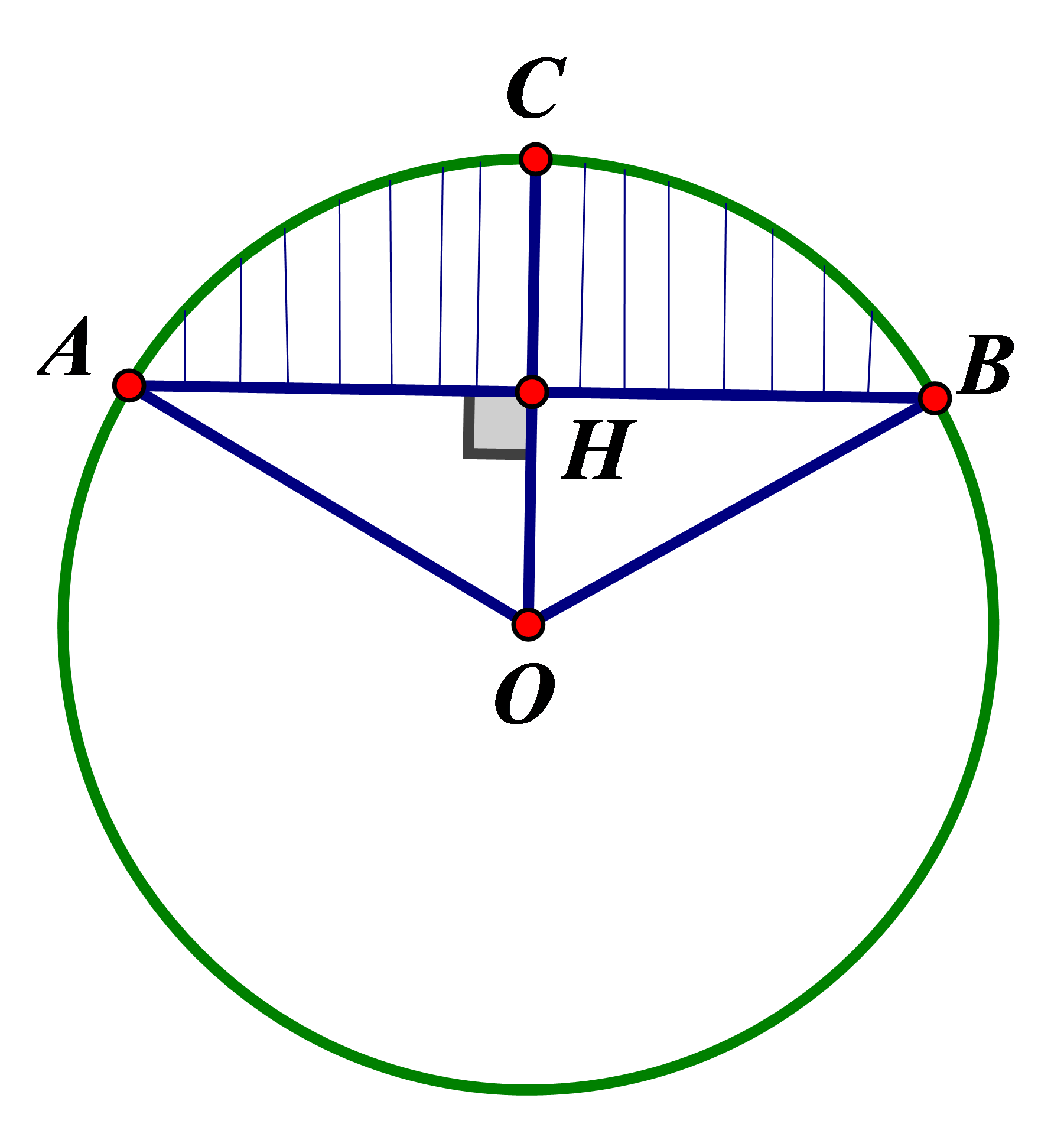
Ta có: $HB = \sqrt {O{B^2} - O{H^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}$$ \Rightarrow AB = 2HB = \sqrt 3 $ $\left( m \right)$
Ta có: ${S_{\Delta OAB}} = \frac{1}{2}AB\,.\,OH = \frac{1}{2}\sqrt 3 \,.\,\frac{1}{2} = \frac{{\sqrt 3 }}{4}$ $\left( {{m^2}} \right)$
Tam giác

OHB

có

\sin \hat{HOB} = \frac{HB}{OB} = \frac{\sqrt{3}}{2} \Rightarrow \hat{HOB} = 60 ° \Rightarrow \hat{AOB} = 2 \hat{HOB} = 120 °

.
Gọi ${S_1}$ là diện tích hình quạt tròn $OACB$, ta có:
${S_1} = \frac{{\pi {R^2}\,.\,120}}{{360}} = \frac{\pi }{3}\,\,\left( {{m^2}} \right)$
Gọi ${S_2}$ là diện tích hình viên phân giới hạn bởi dây $AB$ và cung nhỏ , ta có:
${S_2} = {S_1} - {S_{\Delta OAB}} = \frac{\pi }{3} - \frac{{\sqrt 3 }}{4} = \frac{{4\pi - 3\sqrt 3 }}{{12}}$ $\left( {{m^2}} \right)$
Thể tích phần dầu đã hút đi là: ${V_1} = \frac{1}{3}{S_2}\,.\,5 = \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{36}}$$\left( {{m^3}} \right)$
Thể tích của thùng dầu là: $V = \frac{1}{3}\pi {R^2}.5 = \frac{{5\pi }}{3}\,\,\left( {{m^3}} \right)$
Thể tích dầu còn lại trong thùng là: ${V_2} = V - {V_1} = \frac{{5\pi }}{3} - \frac{{5\left( {4\pi - 3\sqrt 3 } \right)}}{{36}} \approx 4,21\,\,\left( {{m^3}} \right)$

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bạn Toán đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Học. Một cây lăn sơn tường có dạng một khối trụ với bán kính đáy là $5{\rm{ cm}}$ và chiều cao là $23{\rm{ cm}}$ (hình vẽ bên). Nhà sản xuất cho biết sau khi lăn $1000$ vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn Toán cần mua ít nhất mấy cây lăn sơn tường biết diện tích tường mà bố bạn Toán cần sơn là $100{\rm{ }}{{\rm{m}}^2}$. (Cho $\pi = 3,14$)

Xem đáp án

Lời giải

Đổi $5{\rm{ cm }} = {\rm{ }}0,05{\rm{ m}}$, $23{\rm{ cm }} = {\rm{ }}0,23{\rm{ m}}$.
Diện tích tường được sơn khi lăn cây lăn sơn 1 vòng bằng diện tích xung quanh của hình trụ có bán kính $0,05{\rm{ m}}$ và chiều cao $0,23{\rm{ m}}$.
Diện tích xung quanh của hình trụ bằng:${S_{xq}} = 2\pi rh = 2 \times 3,14 \times 0,05 \times 0,23 = 0,023\pi $ $\left( {{{\rm{m}}^2}} \right)$
Diện tích mỗi cây sơn có thể sơn được là $1000 \times {S_{xq}} = 23\pi {\rm{ }}\left( {{{\rm{m}}^2}} \right)$.
Vì $\frac{{100}}{{23\pi }} \approx 1,38$ nên số cây lăn sơn tối thiểu cần phải mua là $2$ cây.

Câu 2

Ở hai quầy hàng \[A\] và \[B\] trong hội hoa xuân, người ta bán hai loại bắp rang bơ lần lượt được đựng trong hai loại hộp hình nón và hình trụ với thông tin về giá cả và định lượng như trong hình dưới đây. Vỏ hộp được làm bằng giấy, phần này nhận được tài trợ của công ty giấy, nên cả hai quầy không tốn chi phí làm vỏ hộp. Hỏi bạn \[H\] nên mua bắp rang bơ ở quầy \[A\] hay quầy \[B\] để bạn có lợi hơn? Tại sao?

Xem đáp án

Lời giải

Ta có: \[{V_A} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}.\pi {.3^2}.6 = 18\pi \]
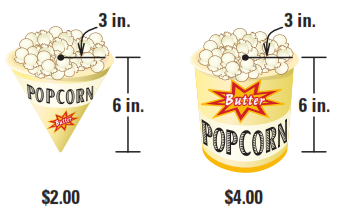
\[\begin{array}{l}{V_{\bf{B}}} = \pi {r^2}h = \pi {.3^2}.6 = 54\pi \\ \Rightarrow {V_B} = 3{V_A}\end{array}\]
Mà giá quầy hàng \[B\] gấp \[2\] lần giá quầy hàng \[A\]
Vậy bạn \[H\] nên mua bắp rang bơ ở quầy \[B\] thì có lợi hơn

Câu 3