Để tạo một mô hình kim tự tháp (hình chóp tứ giác đều) từ tấm bìa, bạn Hạ cắt theo hình bên (ở giữa là hình vuông cạnh 4 dm, các tam giác bên ngoài là tam giác cân có chiều cao 3 dm) rồi gấp 4 tam giác lại chung đỉnh. Hãy tính thể tích của mô hình được tạo thành ở trên (làm tròn đến 1 chữ số thập phân)


Câu hỏi trong đề: 123 bài tập Nón trụ cầu và hình khối có lời giải !!
Quảng cáo
Trả lời:
Độ dài đường chéo của mặt đáy là: \(\sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2 \) \(\left( {dm} \right)\)
Chiều cao của hình chóp là \(h = \sqrt {13 - 8} = \sqrt 5 \) (dm)
Diện tích đáy của hình chóp là \(S = 4.4 = 16\) \(\left( {d{m^2}} \right)\)
Vậy thể tích của hình chóp là: \(V = \frac{1}{3}S.h \Rightarrow V = \frac{{16\sqrt 5 }}{3} \approx 11,9\)\(\left( {d{m^3}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích tường được sơn khi lăn cây lăn sơn 1 vòng bằng diện tích xung quanh của hình trụ có bán kính \(0,05{\rm{ m}}\) và chiều cao \(0,23{\rm{ m}}\).
Diện tích xung quanh của hình trụ bằng:\({S_{xq}} = 2\pi rh = 2 \times 3,14 \times 0,05 \times 0,23 = 0,023\pi \) \(\left( {{{\rm{m}}^2}} \right)\)
Diện tích mỗi cây sơn có thể sơn được là \(1000 \times {S_{xq}} = 23\pi {\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vì \(\frac{{100}}{{23\pi }} \approx 1,38\) nên số cây lăn sơn tối thiểu cần phải mua là \(2\) cây.
Lời giải
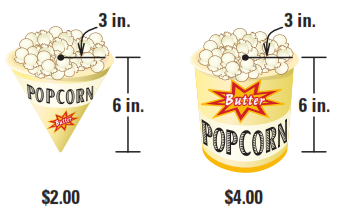
\[\begin{array}{l}{V_{\bf{B}}} = \pi {r^2}h = \pi {.3^2}.6 = 54\pi \\ \Rightarrow {V_B} = 3{V_A}\end{array}\]
Mà giá quầy hàng \[B\] gấp \[2\] lần giá quầy hàng \[A\]
Vậy bạn \[H\] nên mua bắp rang bơ ở quầy \[B\] thì có lợi hơn
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.