Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình: \[AH = 1,2\,m\]; \[BC = 3,2\,m\]; \[CC' = 5\,m\]).
a) Tính thể tích khoảng không ở bên trong lều.
b) Cần phải có ít nhất bao nhiêu m2 vải bạt để dựng lều đó?(Không tính các mép và nếp gấp của lều)
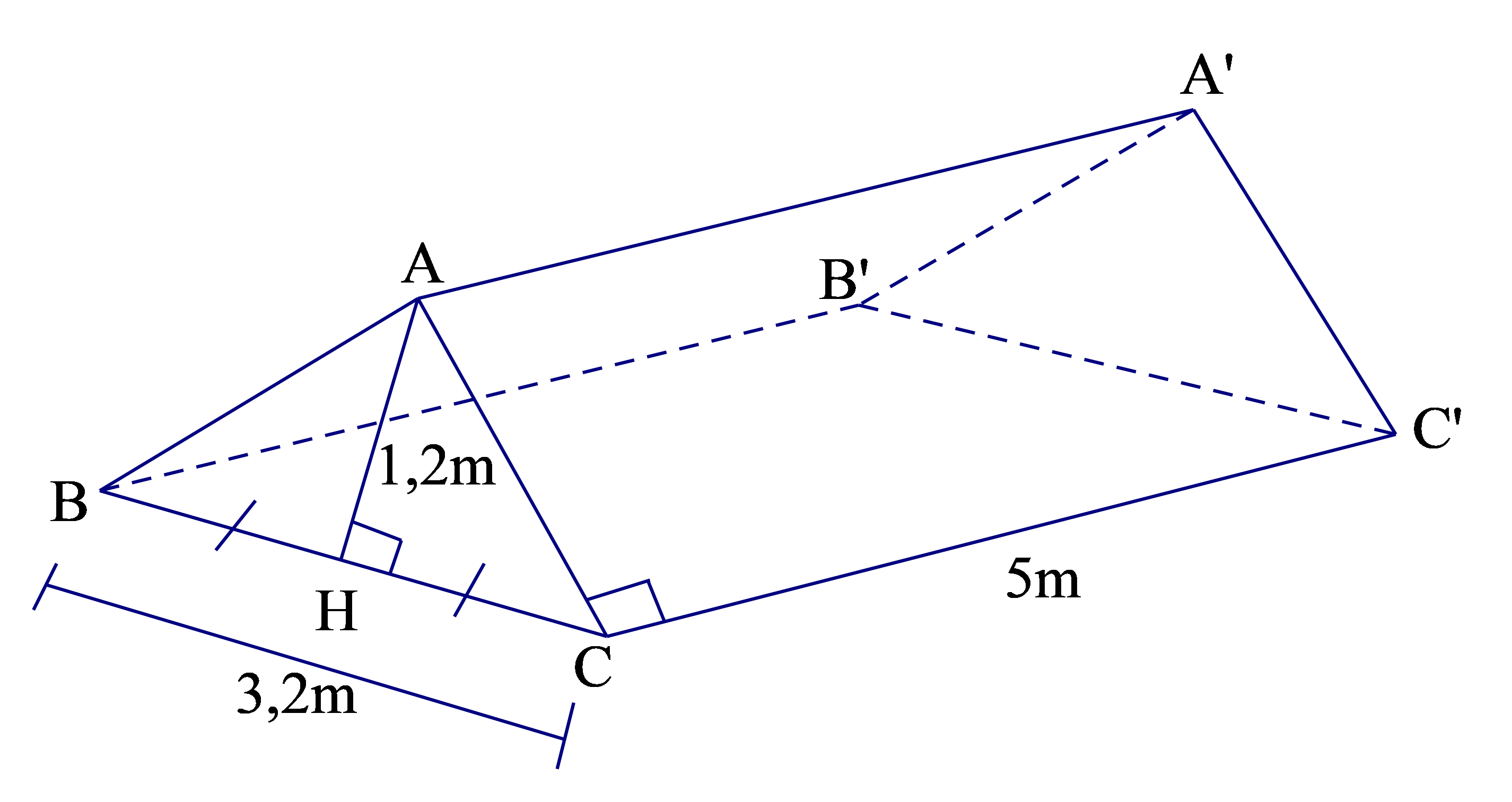
a) Tính thể tích khoảng không ở bên trong lều.
b) Cần phải có ít nhất bao nhiêu m2 vải bạt để dựng lều đó?(Không tính các mép và nếp gấp của lều)

Câu hỏi trong đề: 123 bài tập Nón trụ cầu và hình khối có lời giải !!
Quảng cáo
Trả lời:
Thể tích khoảng không ở bên trong lều \(V = S.h = 1,92.5 = 9,6\left( {{m^3}} \right)\)
b) Áp dụng định lí Pytago vào tam giác vuông \(AHC\), ta tính được AC = 2m
Số m2 vải bạt ít nhất cần có: \(2.(1,92 + 2.5) = 23,84{m^2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích tường được sơn khi lăn cây lăn sơn 1 vòng bằng diện tích xung quanh của hình trụ có bán kính \(0,05{\rm{ m}}\) và chiều cao \(0,23{\rm{ m}}\).
Diện tích xung quanh của hình trụ bằng:\({S_{xq}} = 2\pi rh = 2 \times 3,14 \times 0,05 \times 0,23 = 0,023\pi \) \(\left( {{{\rm{m}}^2}} \right)\)
Diện tích mỗi cây sơn có thể sơn được là \(1000 \times {S_{xq}} = 23\pi {\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vì \(\frac{{100}}{{23\pi }} \approx 1,38\) nên số cây lăn sơn tối thiểu cần phải mua là \(2\) cây.
Lời giải
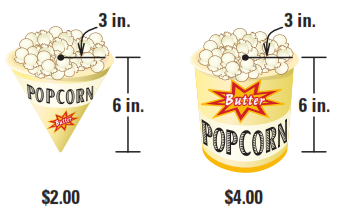
\[\begin{array}{l}{V_{\bf{B}}} = \pi {r^2}h = \pi {.3^2}.6 = 54\pi \\ \Rightarrow {V_B} = 3{V_A}\end{array}\]
Mà giá quầy hàng \[B\] gấp \[2\] lần giá quầy hàng \[A\]
Vậy bạn \[H\] nên mua bắp rang bơ ở quầy \[B\] thì có lợi hơn
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.