Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức \[f(x) = 0,01{x^3} - 0,04{x^2} + 0,25x + 0,44\] (tỉ USD) với x là số năm tính từ 2010 đến 2017 \[(0 \le x \le 7)\]. (Theo: https://infographics.vn/interactive-xuat-khau-rau-qua- du-bao-bung-no-dat-4-ty-usd-trong-nam-2023/116220.vna)
a) Tính đạo hàm của hàm số y = f (x).
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức \[f(x) = 0,01{x^3} - 0,04{x^2} + 0,25x + 0,44\] (tỉ USD) với x là số năm tính từ 2010 đến 2017 \[(0 \le x \le 7)\]. (Theo: https://infographics.vn/interactive-xuat-khau-rau-qua- du-bao-bung-no-dat-4-ty-usd-trong-nam-2023/116220.vna)
a) Tính đạo hàm của hàm số y = f (x).
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Quảng cáo
Trả lời:
a) \({y^\prime } = {f^\prime }(x) = 0,03{x^2} - 0,08x + 0,25\)
b) Tập xác định: \(D = [0;7]\)
Ta có: \({y^\prime } = {f^\prime }(x) > 0\forall x \in \mathbb{R}\) nên \(y = f(x)\) luôn đồng biến \(\forall x \in [0;7]\)
Vậy kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
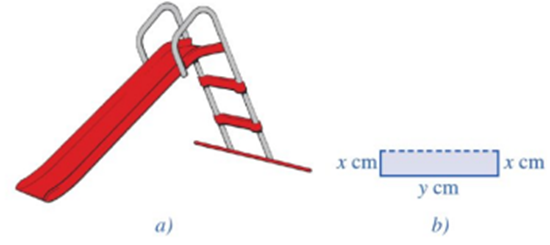
a) Do tấm kim loại có bề rộng 80 cm nên ta có: 2x + y = 80\[ \Leftrightarrow \]y = 80 – 2x.
Để có thể thiết kế được máng trượt thì y > 0\[ \Leftrightarrow \]80−2x > 0\[ \Leftrightarrow \]x < 40.
Suy ra 0 < x < 40.
Diện tích của mặt cắt máng trượt là: S = xy = x(80 – 2x) = −2x2 + 80x.
b) Ta có: S(x) = − 2x2 + 80x với x \[ \in \] (0 ; 40);
S'(x)= − 4x+80;
S'(x)=0\[ \Leftrightarrow \]− 4x + 80=0\[ \Leftrightarrow \]x = 20.
Bảng biến thiên của hàm số S(x) như sau:
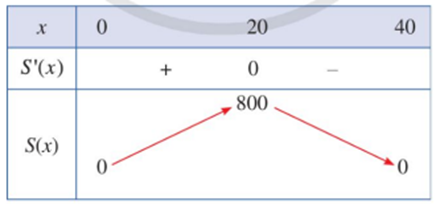
Do đó, hàm số S(x) đạt cực đại tại x = 20 và SCĐ = 80.
Vậy để cầu trượt đảm bảo an toàn nhất cho trẻ em thì x = 20 cm.
Lời giải
Ta có: \({f^\prime }(t) = \frac{{ - 5000\left( {1 + 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}} = \frac{{25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\)
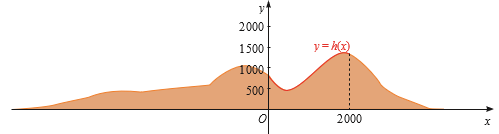
Tốc độ bán hàng là lớn nhất khi \({f^\prime }(t)\) lớn nhất. Đặt \(h(t) = \frac{{25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\).
\({h^\prime }(t) = \frac{{ - 25000{e^{ - t}}{{\left( {1 + 5{e^{ - t}}} \right)}^2} - 2 \cdot \left( { - 5{e^{ - t}}} \right) \cdot \left( {1 + 5{e^{ - t}}} \right) \cdot 25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}}\)
\( = \frac{{ - 25000{e^{ - t}}\left( {1 + 5{e^{ - t}}} \right)\left( {1 + 5{e^{ - t}} - 10{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}} = \frac{{ - 25000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} \Leftrightarrow {h^\prime }(t) = 0\)
\( \Leftrightarrow \frac{{ - 25000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} = 0 \Leftrightarrow 1 - 5{e^{ - t}} = 0 \Leftrightarrow {e^{ - t}} = \frac{1}{5} \Leftrightarrow t = \ln 5({\rm{tm}})\)
Ta có bảng biến thiên với \(t \in [0; + \infty )\):
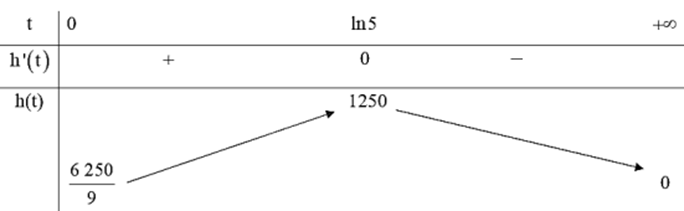
Vậy sau khi phát hành khoảng \(\ln 5 \approx 1,6\) năm thì thì tốc độ bán hàng là lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.