Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \[N(t) = \frac{{25t + 10}}{{t + 5}},t \ge 0\], trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \[\mathop {\lim }\limits_{t \to + \infty } N(t)\]. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \[N(t) = \frac{{25t + 10}}{{t + 5}},t \ge 0\], trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \[\mathop {\lim }\limits_{t \to + \infty } N(t)\]. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Quảng cáo
Trả lời:
a) Dân số của thị trấn đó vào năm 2000 là: \(N(0) = \frac{{25.0 + 10}}{{0 + 5}} = \frac{{10}}{5} = 2\) (nghìn người)
Dân số của thị trấn đó vào năm 2015 là: \(N(15) = \frac{{25.15 + 10}}{{15 + 5}} = 19,25\) (nghìn người)
b) Ta có: \(\mathop {\lim }\limits_{t \to + \infty } N(t) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25t + 10}}{{t + 5}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{25 + \frac{{10}}{t}}}{{1 + \frac{5}{t}}} = 25\)
Vì \(\mathop {\lim }\limits_{t \to + \infty } N(t) = 25\) và nên dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua ngường 25 nghìn người.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
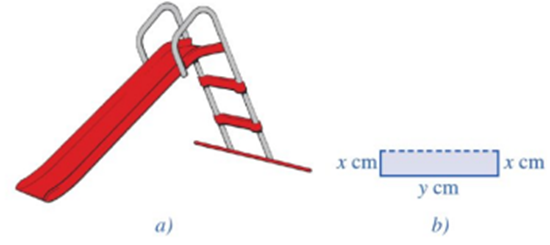
a) Do tấm kim loại có bề rộng 80 cm nên ta có: 2x + y = 80\[ \Leftrightarrow \]y = 80 – 2x.
Để có thể thiết kế được máng trượt thì y > 0\[ \Leftrightarrow \]80−2x > 0\[ \Leftrightarrow \]x < 40.
Suy ra 0 < x < 40.
Diện tích của mặt cắt máng trượt là: S = xy = x(80 – 2x) = −2x2 + 80x.
b) Ta có: S(x) = − 2x2 + 80x với x \[ \in \] (0 ; 40);
S'(x)= − 4x+80;
S'(x)=0\[ \Leftrightarrow \]− 4x + 80=0\[ \Leftrightarrow \]x = 20.
Bảng biến thiên của hàm số S(x) như sau:
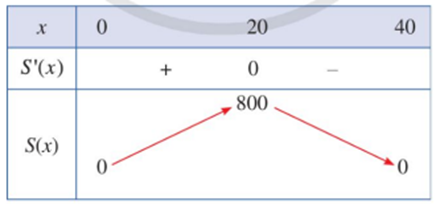
Do đó, hàm số S(x) đạt cực đại tại x = 20 và SCĐ = 80.
Vậy để cầu trượt đảm bảo an toàn nhất cho trẻ em thì x = 20 cm.
Lời giải
Ta có: \({f^\prime }(t) = \frac{{ - 5000\left( {1 + 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}} = \frac{{25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\)
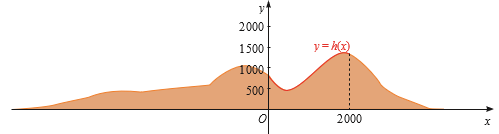
Tốc độ bán hàng là lớn nhất khi \({f^\prime }(t)\) lớn nhất. Đặt \(h(t) = \frac{{25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^2}}}\).
\({h^\prime }(t) = \frac{{ - 25000{e^{ - t}}{{\left( {1 + 5{e^{ - t}}} \right)}^2} - 2 \cdot \left( { - 5{e^{ - t}}} \right) \cdot \left( {1 + 5{e^{ - t}}} \right) \cdot 25000{e^{ - t}}}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}}\)
\( = \frac{{ - 25000{e^{ - t}}\left( {1 + 5{e^{ - t}}} \right)\left( {1 + 5{e^{ - t}} - 10{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^4}}} = \frac{{ - 25000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} \Leftrightarrow {h^\prime }(t) = 0\)
\( \Leftrightarrow \frac{{ - 25000{e^{ - t}}\left( {1 - 5{e^{ - t}}} \right)}}{{{{\left( {1 + 5{e^{ - t}}} \right)}^3}}} = 0 \Leftrightarrow 1 - 5{e^{ - t}} = 0 \Leftrightarrow {e^{ - t}} = \frac{1}{5} \Leftrightarrow t = \ln 5({\rm{tm}})\)
Ta có bảng biến thiên với \(t \in [0; + \infty )\):
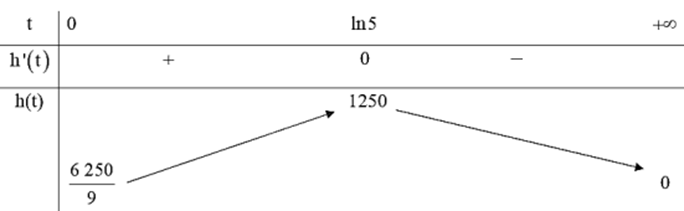
Vậy sau khi phát hành khoảng \(\ln 5 \approx 1,6\) năm thì thì tốc độ bán hàng là lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.