Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: g(x) = \[x + \frac{1}{x}\]
trên khoảng (0; 5);
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: g(x) = \[x + \frac{1}{x}\]
trên khoảng (0; 5);
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét \(g(x) = x + \frac{1}{x}\) trên khoảng \((0;5)\); \({g^\prime }(x) = 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 1({\rm{ lo }}ai)}\end{array}} \right.\)
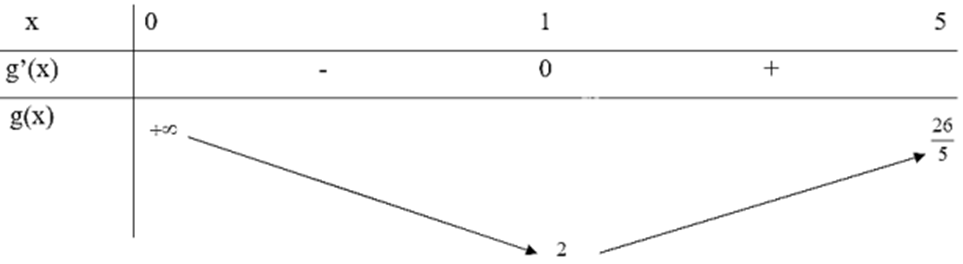
Từ bảng biến thiên, ta thấy \({\min _{(0;5)}}f(x) = f(1) = 2\) và hàm số không tồn tại giá trị lớn nhất trên khoảng \((0;5)\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: f '(x) = 3x2 – 12x + 9; f '(x) = 0 ⇔ x = 1 hoặc x = 3.
Bảng biến thiên của hàm số trên nửa khoảng [–1; +∞):
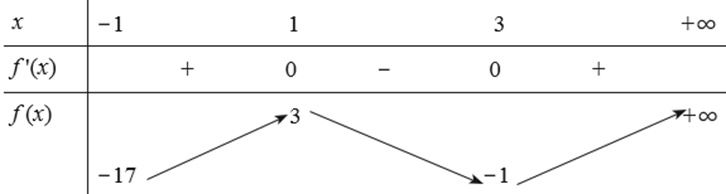
Từ bảng biến thiên, ta thấy \[\mathop {\min }\limits_{\left[ { - 1; + \infty } \right)} \] f (x) = f (–1) = −17 và hàm số không có giá trị lớn nhất trên [−1; +∞).
Nhắn tin Zalo