Tam giác \(ABC\) có đỉnh \(A\left( { - 1;2} \right)\), trực tâm \(H\left( {3;0} \right)\), trung điểm của \(BC\) là \(M\left( {6;1} \right)\). Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Tam giác \(ABC\) có đỉnh \(A\left( { - 1;2} \right)\), trực tâm \(H\left( {3;0} \right)\), trung điểm của \(BC\) là \(M\left( {6;1} \right)\). Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Câu hỏi trong đề: Trắc nghiệm Vecto trong mặt phẳng tọa độ lớp 10 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
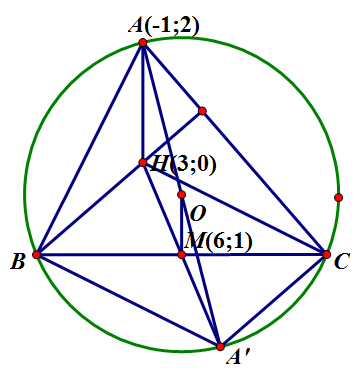
Gọi \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Kẻ đường kính \(AA'\) của đường tròn khi đó ta có \(\widehat {ABA'} = \widehat {ACA'} = 90^\circ \) hay \(A'B \bot AB\) và \(A'C \bot AC\).
Vì \(H\) là trực tâm của tam giác \(ABC\) nên \(BH \bot AC\) và \(CH \bot AB\)\( \Rightarrow BH\,{\rm{//}}\,A'C\) và \(CH\,{\rm{//}}\,A'B\), do đó \(A'BHC\) là hình bình hành. Mà điểm \(M\) là trung điểm của đường chéo \(BC\) nên nó cũng là trung điểm của \(A'H\). Từ đó suy ra \(OM\) là đường trung bình của tam giác \(AHA'\) nên \(\overrightarrow {AH} = 2\overrightarrow {OM} \Leftrightarrow \left\{ \begin{array}{l}4 = 2\left( {6 - {x_O}} \right)\\ - 2 = 2\left( {1 - {y_O}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_O} = 4\\{y_O} = 2\end{array} \right.\)\( \Leftrightarrow O\left( {4;2} \right)\).
Bán kính đường tròn ngoại tiếp tam giác \(ABC\) có độ dài bằng
\(OA = \sqrt {{{\left( { - 1 - 4} \right)}^2} + {{\left( {2 - 2} \right)}^2}} = 5\).
Đáp án: 5.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) \(AC = 8\).
b) Tam giác \(ABC\) cân tại \(B\).
c) \({S_{\Delta ABC}} = 16\sqrt 3 \).
d) \(\widehat {ABC} = 30^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng. \(\overrightarrow {AC} = \left( {4\sqrt 3 ;4} \right) \Rightarrow AC = \sqrt {{{\left( {4\sqrt 3 } \right)}^2} + {4^2}} = 8\).
b) Sai. Ta có \(\overrightarrow {AB} = \left( { - 4\sqrt 3 ;4} \right) \Rightarrow AB = \sqrt {{{\left( { - 4\sqrt 3 } \right)}^2} + {4^2}} = 8\).
Ta thấy \(AB = AC = 8\) nên tam giác \(ABC\) cân tại \(A\).
Lại có \(\overrightarrow {BC} = \left( {8\sqrt 3 ;0} \right) \Rightarrow BC = \sqrt {{{\left( {8\sqrt 3 } \right)}^2} + {0^2}} = 8\sqrt 3 \Rightarrow BC \ne AB\).
Vậy tam giác \(ABC\) không cân tại \(B\).
c) Đúng. Chu vi tam giác \(ABC:2p = AB + AC + BC = 8 + 8 + 8\sqrt 3 = 8\left( {2 + \sqrt 3 } \right)\).
Nửa chu vi tam giác là \(p = 4\left( {2 + \sqrt 3 } \right)\).
Diện tích tam giác: \({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 16\sqrt 3 \).
d) Đúng. Ta có \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB \cdot AC}} = \frac{{{8^2} + {8^2} - {{\left( {8\sqrt 3 } \right)}^2}}}{{2 \cdot 8 \cdot 8}} = - \frac{1}{2} \Rightarrow \widehat {BAC} = 120^\circ \).
Vì tam giác \(ABC\) cân tại \(A\) nên \(\widehat {ABC} = \widehat {ACB} = 30^\circ \).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Ta có \(\overrightarrow c = 5\overrightarrow a - 2\overrightarrow b = 5\left( {3; - 2} \right) - 2\left( {1;4} \right) = \left( {13; - 18} \right)\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập