Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực (đơn vị KJ và làm tròn đến hàng đơn vị) tác động lên xe, biết dốc dài 50 m và nghiêng \(15^\circ \) so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng \(10\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\)).
Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực (đơn vị KJ và làm tròn đến hàng đơn vị) tác động lên xe, biết dốc dài 50 m và nghiêng \(15^\circ \) so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng \(10\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\)).
Quảng cáo
Trả lời:
Trọng lực của ô tô có độ lớn bằng \(\left| {\vec P} \right| = 2500 \times 10 = 25000\) (N).
Trọng lực \(\overrightarrow P \) của ô tô hợp với hướng chuyển dời \(\overrightarrow {MN} \) một góc \(\alpha = 90^\circ + 15^\circ = 105^\circ \).
Trọng lực \(\overrightarrow P \) được phân tích thành hai thành phần \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} :\overrightarrow P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} \), trong đó \(\overrightarrow {{P_1}} \) có phương vuông góc với mặt dốc, \(\overrightarrow {{P_2}} \) có phương song song với mặt dốc.
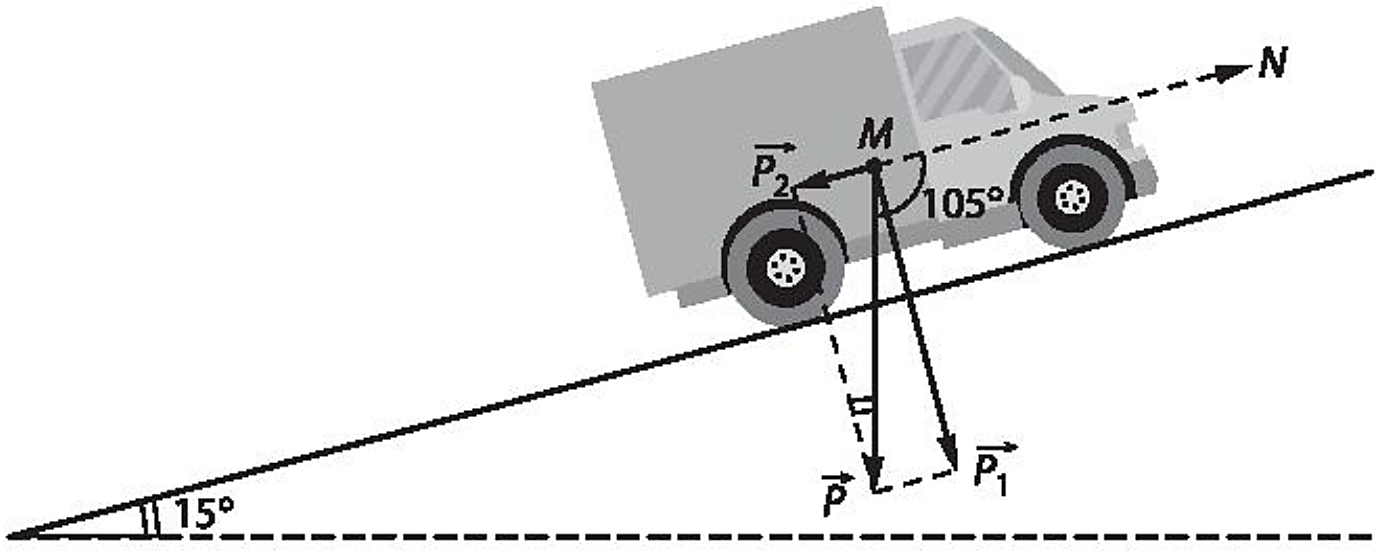
Ta nhận thấy rằng, \(\overrightarrow {{P_1}} \) không có tác dụng đối với chuyển dời \(\overrightarrow {MN} \) của xe, còn \(\overrightarrow {{P_2}} \) ngược hướng với \(\overrightarrow {MN} \). Do đó, công của trọng lực tác động lên xe bằng
\(A = \overrightarrow P \cdot \overrightarrow {MN} = \left| {\overrightarrow P } \right| \cdot \left| {\overrightarrow {MN} } \right| \cdot \cos \left( {\overrightarrow P ,\overrightarrow {MN} } \right) = 25000 \cdot 50 \cdot \cos 105^\circ \approx - 323\,524\) (J) \( \approx - 324\) (KJ).
Đáp án: −324.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
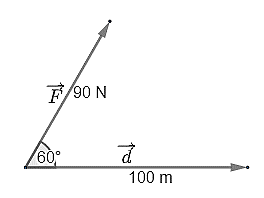
Công sinh bởi lực \(\vec F\) được tính bằng công thức
\(A = \overrightarrow F \cdot \overrightarrow d = \left| {\overrightarrow F } \right| \cdot \left| {\overrightarrow d } \right|{\rm{cos}}\left( {\overrightarrow F ,\overrightarrow d } \right) = 90 \cdot 100 \cdot {\rm{cos}}60^\circ = 4500\,\,\left( {\rm{J}} \right)\).
Vậy công sinh bởi lực \(\vec F\) có độ lớn bằng 4500 (J).
Lời giải
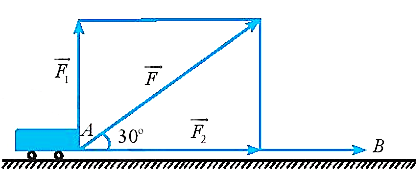
a) Sai. Người thứ nhất kéo một lực là \[40\sqrt 3 \,\,{\rm{(N)}} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = 40\sqrt 3 \], người thứ hai kéo một lực là \[80\,\,{\rm{(N)}} \Rightarrow \left| {\overrightarrow {{F_2}} } \right| = 80\].
b) Đúng. Lực tổng hợp, hợp với phương ngang (mặt đường) một góc \(30^\circ \) và phương lực \(\overrightarrow {{F_2}} \) song song mặt đường nên \(\left( {\overrightarrow {{F_2}} ,\overrightarrow F } \right) = 30^\circ \).
c) Đúng. Ta có lực tổng hợp của hai người là \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
Suy ra độ lớn của \(\overrightarrow F \) là: \(F = \sqrt {{F_1}^2 + {F_2}^2} = 40\sqrt 7 \,{\rm{(N)}}\).
d) Đúng. Công sinh ra khi kéo vật là
\[A = \overrightarrow F \cdot \overrightarrow d = \left| {\overrightarrow F } \right| \cdot \left| {\overrightarrow d } \right| \cdot \cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 40\sqrt 7 \cdot 5 \cdot \cos 30^\circ = 1000\sqrt {21} \,{\rm{(J)}} = a\sqrt b {\rm{(J)}} \Rightarrow \left\{ \begin{array}{l}a = 1000\\b = 21\end{array} \right.\].
Khi đó \(a + b = 1021\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.