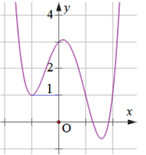
Cho hàm số \[f\left( x \right)\]có đạo hàm \(f'\left( x \right)\)liên tục trên \(R\). Hàm \(f'\left( x \right)\)có đồ thị như hình vẽ.
Các mệnh đề sau đúng hay sai?
a) \[f\left( { - 3} \right) < f\left( { - 2} \right)\]
Cho hàm số \[f\left( x \right)\]có đạo hàm \(f'\left( x \right)\)liên tục trên \(R\). Hàm \(f'\left( x \right)\)có đồ thị như hình vẽ.

Các mệnh đề sau đúng hay sai?
Quảng cáo
Trả lời:
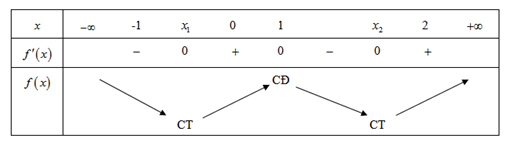
Từ đồ thị hàm số \(f'\left( x \right)\)ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 1\\x = {x_2}\end{array} \right.\)với \( - 1 < {x_1} < 1 < {x_2} < 2\).
Từ đó suy ra bảng biến thiên của hàm số\[f\left( x \right)\] là:
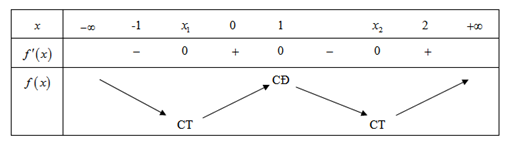
a) Hàm số \[f\left( x \right)\]nghịch biến trên khoảng \[\left( { - \infty \,;\,{x_1}\,} \right)\], \[ - 3 < - 2 < {x_1}\]\[ \Rightarrow f\left( { - 3} \right) > f\left( { - 2} \right)\].Chọn S
Câu hỏi cùng đoạn
Câu 2:
b) Hàm số \[f\left( x \right)\]đồng biến trên khoảng \[\left( { - \infty \,;\, - 1} \right)\].
Từ đồ thị hàm số \(f'\left( x \right)\)ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 1\\x = {x_2}\end{array} \right.\)với \( - 1 < {x_1} < 1 < {x_2} < 2\).
Từ đó suy ra bảng biến thiên của hàm số\[f\left( x \right)\] là:
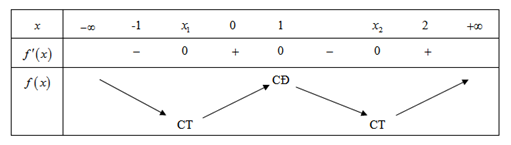
b) Hàm số \[f\left( x \right)\]nghịch biến trên khoảng \[\left( { - \infty \,;\,{x_1}\,} \right)\], \[\left( { - \infty \,;\, - 1} \right) \subset \left( { - \infty \,;\,{x_1}\,} \right)\]\[ \Rightarrow \]hàm số \[f\left( x \right)\] đồng biến trên khoảng \[\left( { - \infty \,;\, - 1} \right)\].Chọn S
Câu 3:
c) \[f\left( 0 \right) < f\left( 1 \right)\].
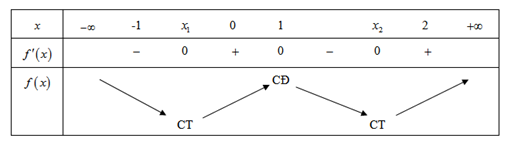
Từ đồ thị hàm số \(f'\left( x \right)\)ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 1\\x = {x_2}\end{array} \right.\)với \( - 1 < {x_1} < 1 < {x_2} < 2\).
Từ đó suy ra bảng biến thiên của hàm số\[f\left( x \right)\] là:
Câu 4:
d) Hàm số \[f\left( x \right)\]đạt cực đại tại \[x = 0\].
Từ đồ thị hàm số \(f'\left( x \right)\)ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 1\\x = {x_2}\end{array} \right.\)với \( - 1 < {x_1} < 1 < {x_2} < 2\).
Từ đó suy ra bảng biến thiên của hàm số\[f\left( x \right)\] là:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ đồ thị của hàm số \(y = f'\left( x \right)\) ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
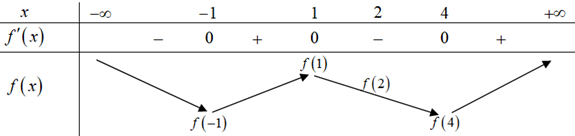
Khi đó dựa vào bảng biến thiên ta thấy:
a) Hàm số có ba điểm cực trị nên Chọn S
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.