Cho nửa đường tròn \[\left( O \right)\] đường kính \[AB = 2R\]. Lấy \[M\] là điểm chính giữa cung \[AB\], hai điểm \[C\] và \[D\] di chuyển trên cung \[MA,MB\] sao cho \[CM//AD\]. Hỏi độ dài cạnh \[CD\] bằng bao nhiêu?
Quảng cáo
Trả lời:
Chọn D
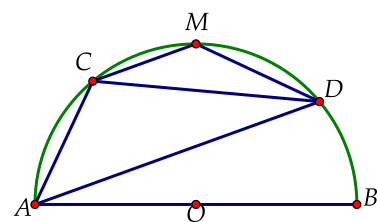
\[M\] là điểm chính giữa của cung \[AB\] nên .
Do \[MC//AD\] nên
\[ \Rightarrow \widehat {COD} = 90^\circ \] (góc ở tâm chắn cung \[CD\])
\[ \Rightarrow \Delta COD\] vuông cân tại \[O \Rightarrow CD = CO\sqrt 2 = R\sqrt 2 \].
Với bài tập này ta cũng có thể lí luận \[ACMD\] là hình thang cân nên \[CD = AM = R\sqrt 2 \].
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
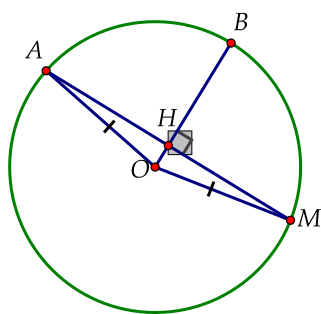
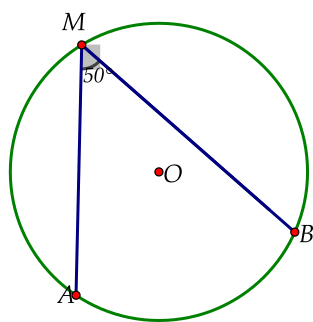
\[\Delta OAM\]cân tại \[O\] \[\left( {OA = OM = R} \right)\].
\[OB \bot AM\]tại \[H\] suy ra \[OB\] đồng thời là đường phân giác của \[\widehat {AOM}\];
\[\widehat {AOB} = \widehat {BOM} = 80^\circ \] \[ \Rightarrow \widehat {AOM} = \widehat {AOB} + \widehat {BOM}\] \[ = 80^\circ + 80^\circ = 160^\circ \].
Do đó số đo của cung nhỏ bằng: \[\widehat {AOM} = 160^\circ \].
Lời giải
Chọn C
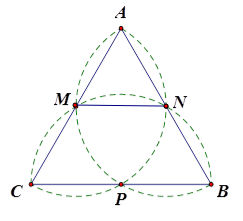
Diện tích tam giác đều \(ABC\) cạnh \(20cm\) là \({S_{\Delta ABC}} = \frac{{{{20}^2}\sqrt 3 }}{4} = 100\sqrt 3 \left( {c{m^2}} \right)\).
Diện tích hình quạt tròn \(MAN\) là \({S_{quatMAN}} = \frac{{\pi {{.10}^2}.60}}{{360}} = \frac{{50\pi }}{3}\left( {c{m^2}} \right)\).
Diện tích tam giác đều \(MAN\) là \({S_{\Delta MAN}} = \frac{{{{10}^2}\sqrt 3 }}{4} = 25\sqrt 3 \left( {c{m^2}} \right)\).
Diện tích hình viên phân \(AN\) là \({S_{quatMAN}} - {S_{\Delta MAN}} = \frac{{50\pi }}{3} - 25\sqrt 3 \left( {c{m^2}} \right)\)
\( \Rightarrow \) Diện tích bông hoa ba cánh bằng tổng diện tích tam giác đều \(ABC\) và \(6\) lần diện tích hình viên phân \(AN\): \(S = 100\sqrt 3 + 6\left( {\frac{{50\pi }}{3} - 25\sqrt 3 } \right) = 100\pi - 50\sqrt 3 \approx 227,6\left( {c{m^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.