Cho hàm số \[y = (2m + 2){x^2}\]. Tìm \[m\] để đồ thị hàm số đi qua điểm \(A(x;y)\) với \((x;y)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\)
Quảng cáo
Trả lời:
Chọn D
Ta có \[\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.\] hay \[\left\{ \begin{array}{l}x = y + 1\\2(y + 1) - y = 3\end{array} \right.\] giải hệ được \[\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right. \Rightarrow A(2;1)\]
Thay \[x = 2;y = 1\] vào hàm số \[y = (2m + 2){x^2}\] ta được
\[1 = (2m + 2){.2^2}\] hay \[2m + 2 = \frac{1}{4}\] suy ra \[m = \frac{{ - 7}}{8}\]. Vậy \[m = - \frac{7}{8}\] là giá trị cần tìm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
Hoành độ giao điểm của đường thẳng \(\left( d \right):y = x + \frac{3}{2}\) và parabol \(\left( P \right):y = \frac{1}{2}{x^2}\) là nghiệm của phương trình
\(\begin{array}{l}\frac{1}{2}{x^2} = x + \frac{3}{2}\\{x^2} - 2x - 3 = 0\\{x^2} - 3x + x - 3 = 0\\x(x - 3) + (x - 3) = 0\\(x - 3)(x + 1) = 0\end{array}\)
\(x - 3 = 0\) hoặc \(x + 1 = 0\)
\(x = 3\) hoặc \(x = - 1\)
D. • Với \(x = - 1\) thì \(y = - 1 + \frac{3}{2} = \frac{1}{2}\) nên \(A\left( { - 1;\frac{1}{2}} \right)\);
A. • Với \(x = 3\) thì \(y = 3 + \frac{3}{2} = \frac{9}{2}\) nên \(B\left( {3;\frac{9}{2}} \right)\)
B. Độ dài đoạn thẳng \(AB = \sqrt {{{\left( { - 1 - 3} \right)}^2} + {{\left( {\frac{1}{2} - \frac{9}{2}} \right)}^2}} = 4\sqrt 2 \).
Lời giải
Chọn D
Phương trình hoành độ giao điểm của (P) và (d) là
Phương trình có \(a + b + c = 1 - m + 1 = 0\)
\(x = 1;x = m\).
Vì vai trò \({x_1};{x_2}\) là như nhau nên ta có
\(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 2022\)
\(\left| 1 \right| + \left| m \right| = 2022\)
\(\left| m \right| = 2021\)
\(m = 2021\) hoặc \(m = - 2021\)
Vậy\(m \in \left\{ { - 2021;2021} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
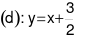 tại hai điểm phân biệt A vàB. Độ dài đoạn thẳng AB bằng
tại hai điểm phân biệt A vàB. Độ dài đoạn thẳng AB bằng cắt parabol
cắt parabol  tại hai điểm phân biệt có hoành độ\({x_1};{x_2}\)thoả mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 2022\) là
tại hai điểm phân biệt có hoành độ\({x_1};{x_2}\)thoả mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 2022\) là