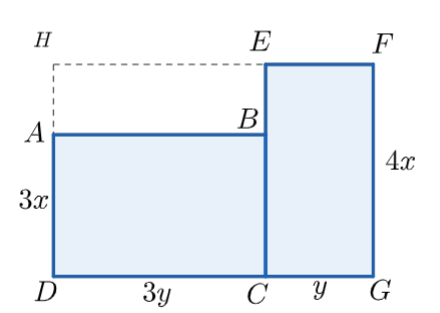
Một mảnh vườn hình chữ nhật với chiều rộng là \(x{\rm{ }}\left( {\rm{m}} \right)\), chiều dài là \(y{\rm{ }}\left( {\rm{m}} \right)\) (với \(y > x > 0\)). Sau khi mở rộng mảnh vườn, ta có chiều rộng mới gấp hai lần chiều rộng ban đầu, chiều dài mới bằng \(\frac{3}{2}\) chiều dài ban đầu của mảnh vườn.
a) Diện tích ban đầu của mảnh vườn là \(xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b) Chiều rộng mới của mảnh vườn khi mở rộng là \(2x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài mới là \(\frac{3}{2}y{\rm{ }}\left( {\rm{m}} \right)\).
c) Diện tích của mảnh vườn sau khi mở rộng là \(3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Diện tích phần được mở rộng thêm của mảnh vườn lớn hơn \(2xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
a) Đúng.
Diện tích ban đầu của mảnh vườn hình chữ nhật là: \(x.y = xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
b) Đúng.
Vì khi mở rộng mảnh vườn, chiều rộng gấp hai lần chiều rộng ban đầu, chiều dài mới bằng \(\frac{3}{2}\) chiều dài ban đầu của mảnh vườn.
Do đó, chiều rộng mới của mảnh vườn khi mở rộng là \(2x{\rm{ }}\left( {\rm{m}} \right),\) chiều dài mới là \(\frac{3}{2}y{\rm{ }}\left( {\rm{m}} \right)\).
c) Đúng.
Diện tích của mảnh vườn sau khi được mở rộng là: \(2x \cdot \frac{3}{2}y = 3xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Sai
Diện tích phần đất được mở rộng thêm của mảnh vườn là: \(3xy - xy = 2xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Vậy diện tích phần được mở rộng thêm của mảnh vườn là \(2xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
a) Đúng.
Thể tích của bể bơi thứ nhất là: \(1,4 \cdot x \cdot y = 1,4xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Đúng.
Diện tích đáy của bể bơi thứ nhất là: \(x \cdot y = xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Mà diện tích đáy của bê bơi thứ hai gấp 3 lần diện tích đáy của bể bơi thứ nhất.
Do đo, diện tích đáy của bể bơi thứ hai là: \(3xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
c) Sai.
Thể tích của bể bơi thứ hai là: \(1,6 \cdot 3xy = 4,8xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Vì \(4,8 < 5\) nên \(4,8xy < 5xy\).
Do đó, thể tích của bể bơi thứ hai nhỏ hơn \(5xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
d) Đúng.
Tổng thể tích hai bể bơi là: \(4,8xy + 1,4xy = 6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Thể tích nước cần bơm đầy hai bể bơi chính bằng tổng thể tích của của hai bể bơi và bằng \(6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
a) Đúng
Ta có \(A = 2{x^2}y + {x^2} + {y^2} + xy - 2{x^2}y\)
\(A = \left( {2{x^2}y - 2{x^2}y} \right) + {x^2} + {y^2} + xy\)
\(A = {x^2} + {y^2} + xy\)
Do đó, thu gọn đa thức \(A\), ta được \(A = {x^2} + xy + {y^2}\).
b) Sai
Vì thu gọn \(A = {x^2} + xy + {y^2}\) nên đa thức \(A\) có bậc là 2.
c) Sai
Ta có \(C = A + B\) nên \(C = {x^2} + xy + {y^2} - 3xy = {x^2} - 2xy + {y^2}\).
d) Đúng
Thay \(x = 24;y = 25\) vào \(C = {x^2} - 2xy + {y^2}\), ta được:
\(C = {24^2} - 2 \cdot 24 \cdot 25 + {25^2} = 576 - 1{\rm{ }}200 + 625 = 1{\rm{ }}201 - 1{\rm{ }}200 = 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(9xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
B. \(16xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
C. \(4xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
D. \(13xy{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập