Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao \[250\]km so với bề mặt của Mặt Trăng. Trong khoảng \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao \(h\) của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) trong đó \(t\) là thời gian tính bằng giây và \(h\) là độ cao tính bằng kilomet.
a) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao lớn nhất mà con tàu đạt được là \(250\)(km).
b) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 25\)(s).
c) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\)(km/s).
d) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao con tàu đạt được khi vận tốc của con tàu lớn nhất là \(139,37\,\)(km).
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao \[250\]km so với bề mặt của Mặt Trăng. Trong khoảng \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao \(h\) của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) trong đó \(t\) là thời gian tính bằng giây và \(h\) là độ cao tính bằng kilomet.
a) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao lớn nhất mà con tàu đạt được là \(250\)(km).
b) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 25\)(s).
c) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\)(km/s).
d) Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao con tàu đạt được khi vận tốc của con tàu lớn nhất là \(139,37\,\)(km).
Câu hỏi trong đề: Đề kiểm tra Toán 12 Kết nối tri thức Chương 1 có đáp án !!
Quảng cáo
Trả lời:
a) Đúng.
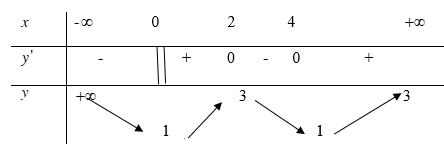
\(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow h'\left( t \right) = - 0,03{t^2} + 2,2t - 30 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 55 \notin \left( {0;50} \right)\\t = 18 \in \left( {0;50} \right)\end{array} \right.\)
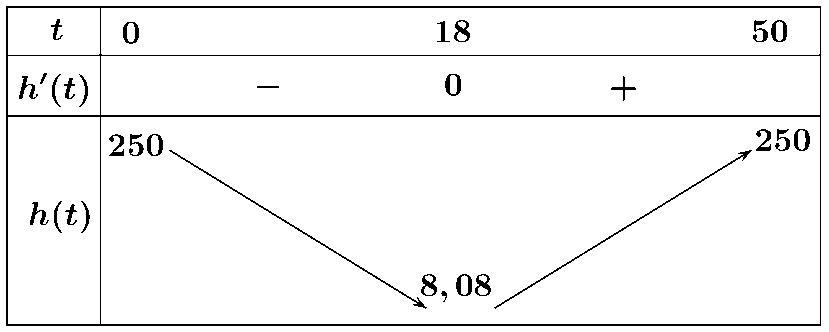
b) Sai. Dựa vào bảng biến thiên trên ta thấy trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 18\left( s \right)\).
c) Đúng. \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow v\left( t \right) = h'\left( t \right) = - 0,03{t^2} + 2,2t - 30\)
\( \Rightarrow a\left( t \right) = v'\left( t \right) = - 0,06t + 2,2 = 0 \Leftrightarrow t \approx 37\)
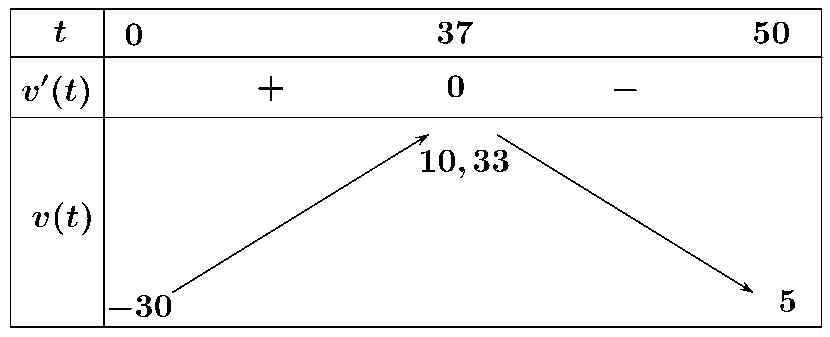
Vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\left( {km/s} \right)\).
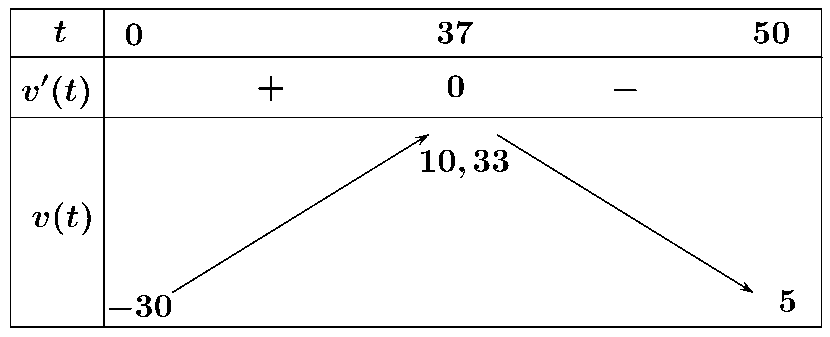
d) Sai. \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250 \Rightarrow v\left( t \right) = h'\left( t \right) = - 0,03{t^2} + 2,2t - 30\)
\( \Rightarrow a\left( t \right) = v'\left( t \right) = - 0,06t + 2,2 = 0 \Leftrightarrow t \approx 37\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
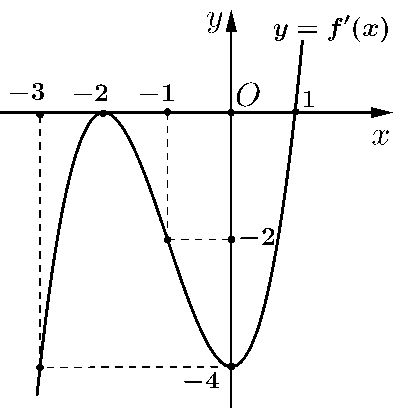
a) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) \ge 0\) với \(\forall x \ge 1\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
b) Sai. Vì từ đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\) chỉ đổi dấu một lần qua \(x = 1\) nên hàm số có một điểm cực trị.
c) Sai. Từ đồ thị ta có hàm số \(f'\left( x \right)\) có dạng: \(f'\left( x \right) = a{\left( {x + 2} \right)^2}\left( {x - 1} \right)\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua \(\left( {0; - 4} \right)\) nên: \( - 4 = a{\left( {0 + 2} \right)^2}\left( {0 - 1} \right) \Leftrightarrow a = 1\).
Vậy \(f'\left( x \right) = {\left( {x + 2} \right)^2}\left( {x - 1} \right) \Rightarrow f'\left( 2 \right) = {\left( {2 + 2} \right)^2}\left( {2 - 1} \right) = 16\).
d) Đúng. Ta có: \(g'\left( x \right) = f'\left( x \right) - x + 1 = 0 \Leftrightarrow f'\left( x \right) = x - 1\).
Vẽ đường thẳng \(y = x - 1\) trên cùng hệ trục tọa độ với đồ thị hàm số \(y = f'\left( x \right)\).
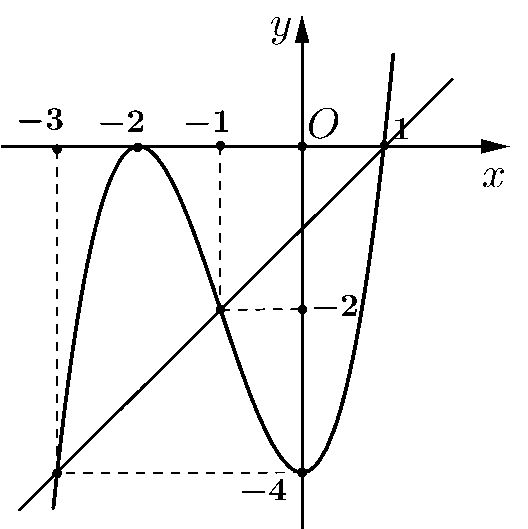
Khi đó: \(f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\\x = 1\end{array} \right.\).
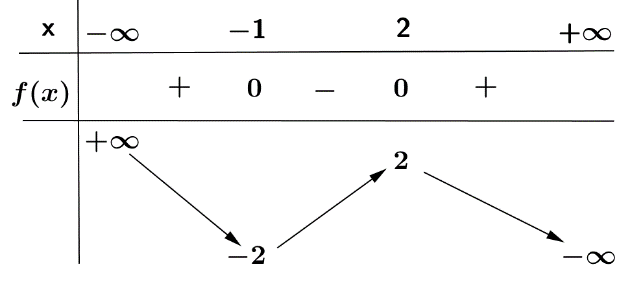
Bảng biến thiên của hàm số \(g\left( x \right)\).

Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) nên \(g\left( x \right)\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Lời giải
Theo đề bài, vận tốc của cá khi bơi trên sông là \(v - 6\), khi đó thời gian để cá bơi đến nơi sinh sản là \(t = \frac{{300}}{{v - 6}}\).
Khi đó, \(E\left( v \right) = c{v^3}\frac{{300}}{{v - 6}}\) với \(v > 6\). Đặt \(x = v - 6\).
Bài năng lượng tiêu hao của cá được tính bởi hàm số:
\[f\left( x \right) = 300c\frac{{{{\left( {x + 6} \right)}^3}}}{x} = 300c\left( {{x^2} + 18x + 108 + \frac{{216}}{x}} \right)\] với \(x > 0\).
Ta có: \[f'\left( x \right) = 300c\left( {2x + 18 - \frac{{216}}{{{x^2}}}} \right) = 0 \Leftrightarrow 2{x^3} + 18{x^2} - 216 = 0 \Rightarrow x = 3\].
Bảng biến thiên:
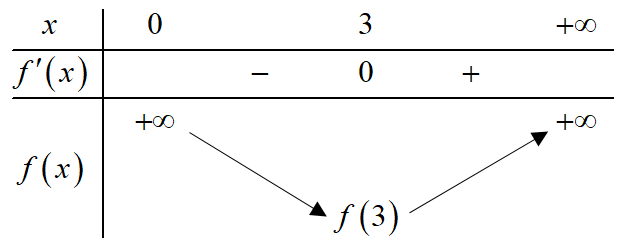
Vậy \(\mathop {\min }\limits_{x \in \left( {0; + \infty } \right)} f\left( x \right) = f\left( 3 \right)\) hay khi vận tốc của cá khi nước đứng yên là \(v = 9km/h\) thì cá ít tốn năng lượng nhất.
Đáp án: 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.