Trong cuộc thi 2 môn phối hợp gồm chèo thuyền và chạy bộ. Các vận động viên sẽ chèo thuyền từ điểm xuất phát \(A\)cách bờ \(BC\)\(6km\) sau đó đến bờ tại một vị trí \(D\) bất kì rồi chạy về đích \(C\),(xem hình minh họa). Biết rằng quãng đường trên bờ \(BC = 15km\), vận tốc chèo thuyền của một vận động viên \(X\)là \(8km/h\) và vận tốc chạy trên bờ là \(16km/h\)
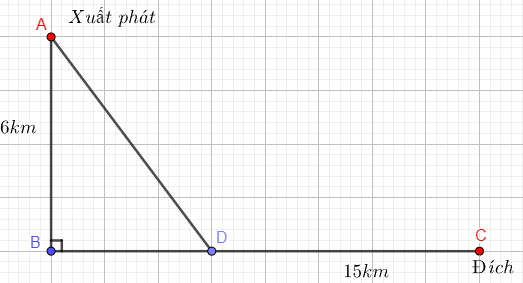
Hỏi \(X\) nên chèo thuyền về bờ tại vị trí \(D\) cách đích \(C\) là bao nhiêu để tổng thời gian về đích là sớm nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp số: \(15 - 2\sqrt 3 \).
Giả sử \(BD = x \Rightarrow \left\{ \begin{array}{l}DC = 15 - x\\AD = \sqrt {{x^2} + 36} \end{array} \right.,\left( {0 \le x \le 15} \right)\).
Tổng thời gian để vận động viên về đích là \(t = \frac{{\sqrt {{x^2} + 36} }}{8} + \frac{{15 - x}}{{16}}\).
Xét hàm số \(f\left( x \right) = \frac{{\sqrt {{x^2} + 36} }}{8} + \frac{{15 - x}}{{16}}\),\(0 \le x \le 15\), ta có \(f'\left( x \right) = \frac{x}{{8\sqrt {{x^2} + 36} }} - \frac{1}{{16}}\).
Ta có bảng biến thiên
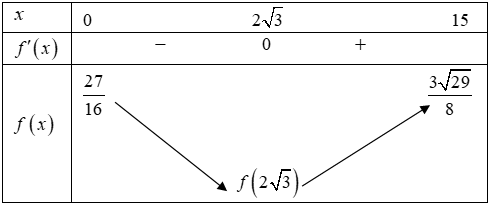
Vậy vận động viên nên vào bờ tại vị trí \(D\) cách đích \(C\) một khoảng là \(15 - 2\sqrt 3 \approx 11,54km\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {1\,;\,3} \right]\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759147890.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
Dựa vào đồ thị hàm số suy ra
a) \(m = - 4\).
b) \(M = 0\).
c)\(M + m = 0 + ( - 4) = - 4\).
d) Với \(\forall x \in \left[ { - 1\,;\, + \infty } \right)\), ta có: \(f\left( x \right) \le 0 \Rightarrow f\left( x \right) + 4 \le 4\) và \(f\left( x \right) + 4 = 4 \Leftrightarrow f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\)
Vậy, giá trị lớn nhất của hàm số \(y = f\left( x \right) + 4\) trên nửa khoảng \(\left[ { - 1\,;\, + \infty } \right)\) là \(4\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
TXĐ: \[D = \mathbb{R}\]
Có \( - 1 \le \sin 2025x \le 1 \Leftrightarrow - 3 \le 3\sin 2025x \le 3 \Leftrightarrow 2 \le 3\sin 2025x + 5 \le 8\)
Suy ra: \(\mathop {{\rm{max}}}\limits_\mathbb{R} y = 8 \Leftrightarrow \sin 2025x = 1 \Leftrightarrow x = \frac{\pi }{{4050}} + \frac{{k2\pi }}{{2025}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập