II. TRẮC NGHIỆM ĐÚNG SAI
[NB-NB-TH-VD] Cho hàm số \(y = f(x) = {x^4} - 2{x^2} - 5\). Các khẳng định sau là đúng hay sai ?
a) Hàm số có 3 điểm cực trị.
b) Hàm số đồng biến trên \(\left( {0; + \infty } \right)\)
c) Điểm \(M\left( {0;1} \right)\) là điểm cực tiểu của đồ thị hàm số \(y = f(x)\).
d) Hàm số \(y = f(x)\) và \(y = f(2x)\) có cùng điểm cực đại.
II. TRẮC NGHIỆM ĐÚNG SAI
[NB-NB-TH-VD] Cho hàm số \(y = f(x) = {x^4} - 2{x^2} - 5\). Các khẳng định sau là đúng hay sai ?
a) Hàm số có 3 điểm cực trị.
b) Hàm số đồng biến trên \(\left( {0; + \infty } \right)\)
c) Điểm \(M\left( {0;1} \right)\) là điểm cực tiểu của đồ thị hàm số \(y = f(x)\).
d) Hàm số \(y = f(x)\) và \(y = f(2x)\) có cùng điểm cực đại.
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 1 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tập xác định \(D = \mathbb{R}\).
\(y' = f'(x) = 4{x^3} - 4x\).
Cho \(y' = 0 \Leftrightarrow x = - 1 \vee x = 0 \vee x = 1.\)
Ta có bảng biến thiên:
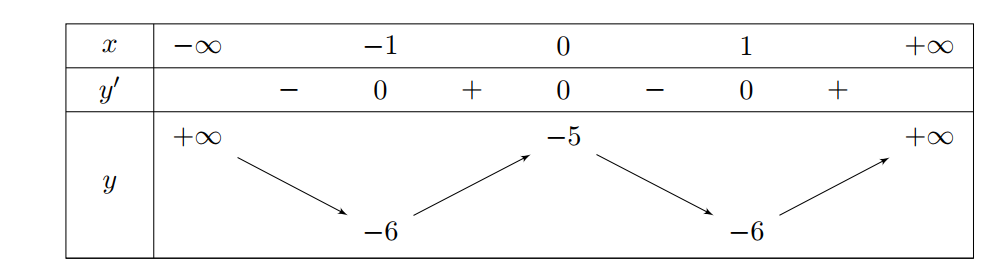
Từ bảng biến thiên ta thấy
a) Đúng.
b) Sai.
c) Sai.
d) Đúng.Ta có
\[\begin{array}{l}f(2x) = 16{x^4} - 8{x^2} - 5\\ \Rightarrow f'(2x) = 64{x^3} - 16x\end{array}\]
Cho \(f'(2x) = 0 \Leftrightarrow x = \frac{{ - 1}}{2} \vee x = 0 \vee x = \frac{1}{2}\)
Ta có bảng biến thiên sau:
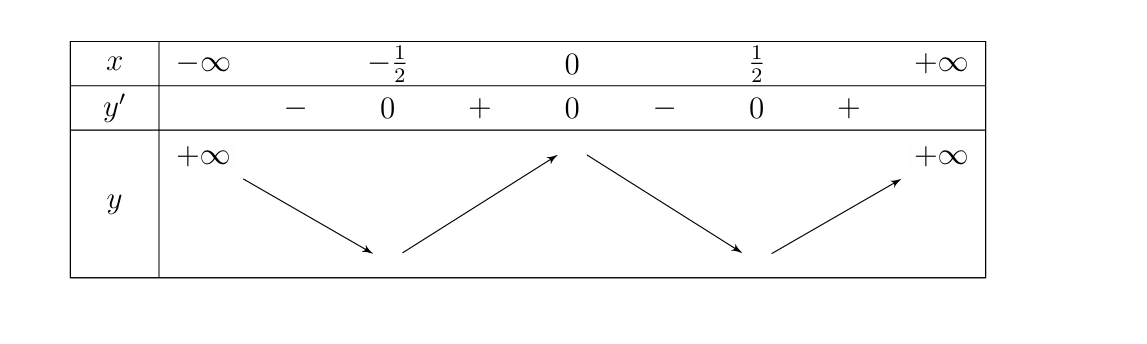
Ta thấy hàm \(y = f(x)\) và \[y = f(2x)\] đều đạt cực đại tại \(x = 0\).
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(y = {x^3} - 2024x\).
B. \(y = - {x^3} + 3x\).
C. \(y = {x^3} - 3{x^2} + 2024\).
D. \(y = - {x^3} + 3{x^2} - 2\).
Lời giải
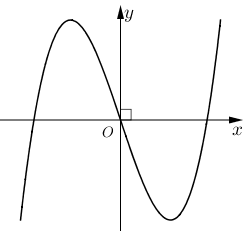
Đường cong có dạng của đồ thị hàm số bậc \(3\) với hệ số \(a > 0\) và đi qua gốc tọa độ \(O\) nên chỉ có hàm số \(y = {x^3} - 2024x\) thỏa mãn yêu cầu bài toán.
Câu 2
A. \(\left( { - \infty ; - 1} \right)\).
B. \(\left( {0;1} \right)\).
C. \(\left( { - 1;1} \right)\).
D. \(\left( { - 1;0} \right)\)
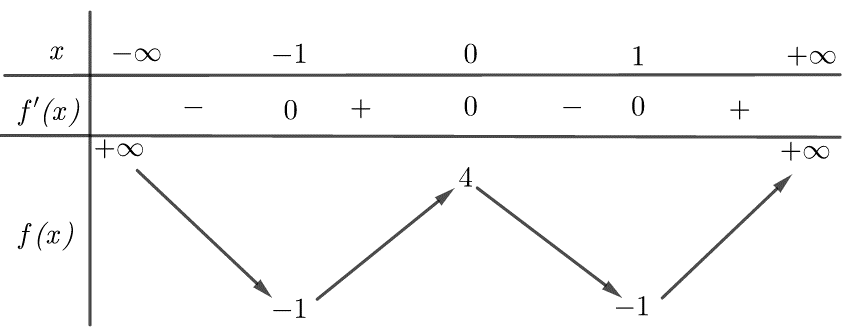
Lời giải
Hàm số đã cho đồng biến trên khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Câu 3
A. \[\left( {0\,;\, - 2} \right)\].
B. \(\left( {2\,;\,0} \right)\).
C. \(\left( { - 2\,;\,0} \right)\).
D. \(\left( {0\,;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[ - 4\].
B. \(4\).
C. \( - 5\).
D. \[5\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
![Cho hàm số \[f\left( x \right)\] có đồ thị trên \[\left[ { - 3;3} \right]\] như hình vẽ. Giá trị lớn nhất \[M\] và gi (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/5-1759221460.png)
A. \[M = 3;m = - 1\].
B. \[M = 4;m = - 2\].
C. \[M = 3;m = - 3\].
D. \[M = - 1;m = 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[1\].
B. \[3\].
C. \(2\).
D. \[4\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo