Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã nhận thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng là \(P\left( n \right) = 800 - 20n\,\,\left( g \right)\). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 1 (có lời giải) !!
Quảng cáo
Trả lời:
Gọi \(F\left( n \right)\) là hàm cân nặng của \(n\) con cá sau vụ thu hoạch trên một đơn vị diện tích.
Ta có: \(F\left( n \right) = \left( {800 - 20n} \right).n = 800n - 20{n^2}\).
Để sau một vụ thu hoạch được nhiều cá nhất thì cân nặng của \(n\) con cá trên một đơn vị diện tích của mặt hồ là lớn nhất.
Bài toán trở thành tìm \(n \in {\mathbb{N}^*}\) sao cho \(F\left( n \right)\) đạt GTLN.
\(\begin{array}{l}F'\left( n \right) = 800 - 40n\\F'\left( n \right) = 0 \Leftrightarrow 800 - 40n = 0 \Leftrightarrow n = 20\end{array}\)
Ta có bảng biến thiên:
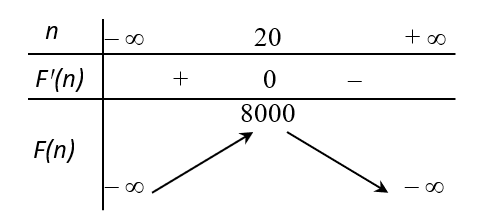
Vậy phải thả \[20\] con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Ta có \[a = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{ - {x^2} - 3x + 4}}{{x + 2}}:x} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} - 3x + 4}}{{{x^2} + 2x}} = - 1,\,\]
\[\,b = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{ - {x^2} - 3x + 4}}{{x + 2}} - \left( { - 1} \right)x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 4}}{{x + 2}} = - 1\]
(Tương tự, \[\mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 3x + 4}}{{x + 2}}:x} \right) = - 1,\,\]\[\mathop {\lim }\limits_{x \to - \infty } \left[ {\frac{{ - {x^2} - 3x + 4}}{{x + 2}} - \left( { - 1} \right)x} \right] = - 1\])
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x + 2}}\) là đường thẳng có phương trình \(y = - x - 1.\)
Câu 2
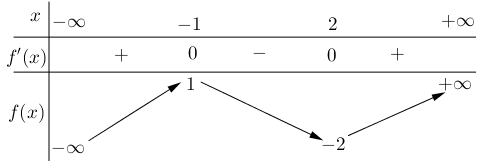
Lời giải
Dựa vào bảng biến thiên, ta có giá trị cực tiểu của hàm số đã cho bằng \( - 2.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số trên đoạn \(\left[ {0\,;\,3} \right]\) bằng A. \(4\). B. \(2\). C. \(3\). D. \(0\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759222372.png)
![Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên \[\mathbb{R}\] bằng A. \(6\). B. \(9\). C. \( - 3\). D. \( - 1\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759222314.png)