PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN

Cho hàm số \(y = \frac{{2{x^2} + 5x + 4}}{{x + 2}}\). Độ dài của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số bằng.

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có đồ thị như hình vẽ :

Xét tính đúng sai của các khẳng định sau:

a) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).

b) Hàm số đạt cực đại tại \(x = 0\).

c) Giá trị nhỏ nhất của hàm số trên \(\left[ { - 1;1} \right]\) bằng \( - 4\).

d) Hàm số \(g\left( x \right) = f\left( {3 - x} \right)\) nghịch biến trên \(\left( {2;5} \right)\).

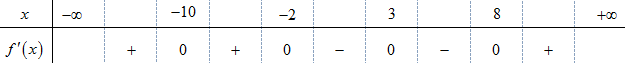
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm \[f'\left( x \right)\] như hình bên dưới.

Xét tính đúng sau của các mệnh đề sau:

a. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0;1} \right)\).

b. Hàm số đã cho nghịch biến trên khoảng \(\left( {3; + \infty } \right)\).

c. Hàm số đã cho có \(2\) điểm cực trị.

d. Hàm số đã cho đạt cực tiểu tại điểm \[x = 0\].

Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(y = f\left( x \right) = \frac{{3x - 1}}{{x - 3}}\) trên đoạn\(\left[ {0;\;2} \right]\). Xét tính đúng sai của các mệnh đề sau:

a. Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\)

b. \(M = \mathop {{\rm{max}}y}\limits_{\left[ {0;\;2} \right]}  = f\left( 1 \right) = \frac{1}{3}\)

c. \(m = \mathop {{\rm{min}}y}\limits_{\left[ {0;\;2} \right]}  = f\left( 2 \right) =  - 5\)

d. \(P = M.m =  - \frac{5}{3}.\)

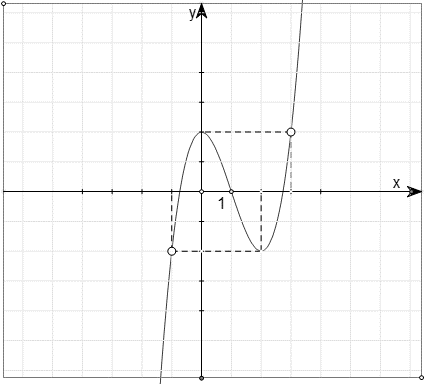
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), có bảng biến thiên như sau: